Оглавление:
Вращение твердого тела вокруг неподвижной оси
Вращательным движением называется такое движение твердого тела, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, остаются неподвижными.
Для того чтобы осуществить вращательное движение тела, достаточно закрепить неподвижно две какие-нибудь его точки, например, при помощи подшипника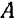 
и подпятника 
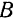(рис. 117), тогда прямая, проходящая через эти две точки, будет осью вращения тела.
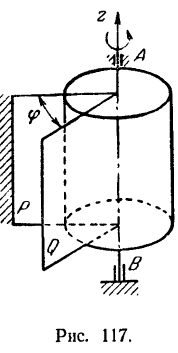
При вращательном движении тела различные его точки движутся, вообще говоря, по-разному. Однако и для вращательного движения можно отыскать такие кинематические характеристики, которые были бы общими для всех точек тела.
Пусть какое-нибудь твердое тело (изображенное для простоты на рис. 117 в виде цилиндра) вращается вокруг неподвижной оси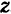 
. Проведем через ось вращения 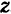неподвижную полуплоскость 
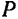и полуплоскость 
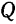, неизменно связанную с вращающимся телом.
Угол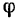 
между неподвижной полуплоскостью, проходящей через ось вращения, и полуплоскостью, неизменно связанной с вращающимся телом и также проходящей через ось вращения, называется углом поворота или угловым перемещением данного тела.
Установим на оси вращения 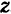положительное направление и условимся считать угол поворота тела положительным, когда он отсчитывается от неподвижной плоскости 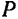в сторону, противоположную ходу часовой стрелки, если смотреть на него с положительного конца оси вращения. Заданием величины и знака угла поворота вполне определяется положение полуплоскости 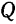и неизменно связанного с ней вращающегося тела.
При вращении тела вокруг оси 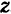угол поворота тела изменяется с течением времени, следовательно, он является некоторой функцией времени
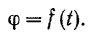
Уравнение (77), устанавливающее зависимость между углом поворота тела и временем его движения, называется уравнением вращательного движения тела.
Угол поворота в механике обычно измеряют в отвлеченных единицах, т. е. в радианах. Иногда в практических задачах угол поворота выражают числом оборотов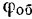 
тела. Так как за один оборот тело поворачивается на угол в 
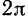радиан, то 
.
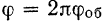Мера изменения угла поворота тела с течением времени называется его угловой скоростью.
Пусть в момент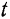 
положение тела определяется углом поворота 
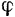, а в момент 
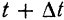— углом поворота 
.
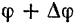Отношение приращения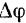 
угла поворота тела за некоторый промежуток времени 
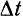к величине этого промежутка времени называется средней за данный промежуток времени угловой скоростью тела.
Обозначая среднюю угловую скорость тела через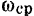 
, будем иметь:
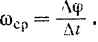
Очевидно, что угловая скорость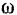 
тела в данный момент равна пределу его средней угловой скорости за промежуток времени, начинающийся в этот момент, когда величина промежутка времени стремится к нулю:
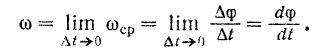
Угловая скорость тела в данный момент равна производной от угла поворота тела по времени.
Значение угловой скорости тела может быть положительным или отрицательным в зависимости от того, в какую сторону вращается тело. Когда тело вращается против часовой стрелки, если смотреть с положительного конца оси вращения, то
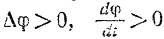
и угловая скорость 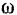положительна. Если тело вращается по часовой стрелке, то угловая скорость отрицательна. Следовательно, знак угловой скорости указывает, в какую сторону в данный момент вращается тело, Размерность угловой скорости
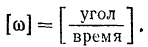
Так как угол в механике измеряется обычно в радианах, а время в секундах, то угловая скорость измеряется в радианах в секунду. Единица угловой скорости обозначается при этом так: рад/сек.
На практике часто угловую скорость тела выражают не в радианах в секунду, а в оборотах в минуту. При этом обычно угловую скорость, выраженную числом оборотов в минуту, обозначают буквой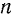 
. Нетрудно найти зависимость между 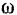и 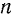. Так как один оборот тела соответствует его повороту на угол в 
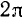радиан, то
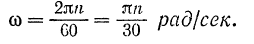
Нужно помнить, что в формуле (80) всегда со выражается в рад/сек, а 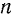— в об/мин.
Если тело вращается неравномерно, то его угловая скорость со изменяется с течением времени и является, следовательно, также некоторой функцией времени
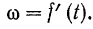
Величина, характеризующая изменение угловой скорости тела с течением времени, называется его угловым ускорением.
Пусть в момент времени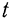 
тело имело угловую скорость 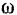, а в момент 
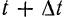— угловую скорость 
.
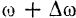Отношение приращения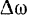 
угловой скорости тела за промежуток времени 
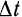к этому промежутку времени называется средним угловым ускорением тела за этот промежуток времени .
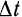Обозначая среднее угловое ускорение тела через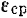 
, будем иметь:
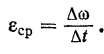
При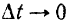 
среднее угловое ускорение приближается к пределу, называемому мгновенным угловым ускорением тела.
Обозначая угловое ускорение тела в данный момент буквой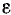 
, будем иметь:
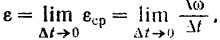
Угловое ускорение тела в данный момент равно первой производной от угловой скорости тела по времени или второй производной от угла его поворота по времени
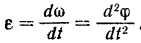
Если знаки угловой скорости и углового ускорения тела совпадают, то его угловая скорость увеличивается но абсолютному значению и тело, следовательно, вращается ускоренно. Если же знаки их различны, то угловая скорость уменьшается по абсолютному значению к тело вращается замедленно.
Размерность углового ускорения
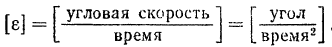
Пример задачи:
Вращение диска вокруг неподвижном оси определяется уравнением
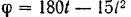
Найти угловую скорость 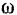и угловое ускорение 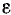диска в моменты времени
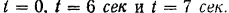
Решение:
Угловую скорость диска находим по формуле (70)
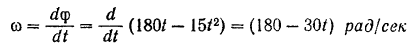
при
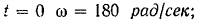
при
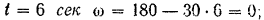
при
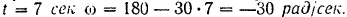
Угловое ускорение диска находим по формуле (82)
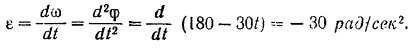
В начальный момент угловая скорость и угловое ускорение диска имеют разные знаки, следовательно, диск вращающийся замедленно. При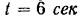 
угловая скорость диска проходит через нуль, после чего он начинает вращаться ускоренно.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
