Вращение твердого тела вокруг неподвижной оси
Рассмотрим твердое тело, у которого неподвижно закреплены две точки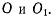 
Такое твердое тело может вращаться вокруг неподвижной оси и не может совершать других движений. При вращении твердого тела всякая его точка описывает окружность в плоскости, перпендикулярной к оси вращения. Радиус соответствующей окружности равен расстоянию точки от оси вращения. Величина скорости произвольной точки твердого тела пропорциональна расстоянию h от этой точки до оси вращения. Положение точки можно определить углом 
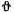(двугранный угол) между двумя плоскостями, проходящими через ось вращения, одна из которых неподвижна, а вторая вращается вместе с рассматриваемой точкой (рис. 44). Численная величина скорости точки М в ее круговом движении равна
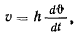
где величина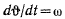 
называется угловой скоростью вращения твердого тела. Она определяет скорость изменения угла между плоскостью, проходящей через ось вращения и через точку М, и неподвижной плоскостью, также проходящей через ось вращения. Таким образом, вращение твердого тела может быть определено так же, как и скользящий вектор, тремя элементами: осью вращения, величиной вращения (величиной угловой скорости вращения) и стороной вращения. Если теперь ввести на оси вращения вектор 
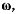направленный в ту сторону, откуда вращение видно происходящим против движения часовой стрелки, а по величине равный величине угловой скорости вращения, то скорость точки М можно будет определить как момент вектора 
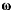относительно точки М. Величина и направление скорости v не изменяются, если перемещать вектор 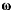вдоль оси вращения, т. е. 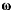— скользящий
вектор
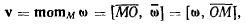
или
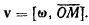
Полученная формула носит название формулы Эйлера. Выберем систему осей Oxyz, начало которой находится на оси вращения. Через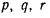 
обозначим проекции вектора угловой скорости 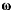на оси координат, а через 
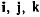— орты координатных осей. Тогда из формулы Эйлера получим
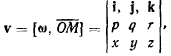
откуда
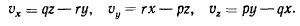
Если ось вращения проходит через точку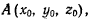 
то для
определения скоростей точек твердого тела формула Эйлера дает
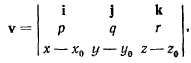
или
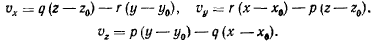
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Элементарные движения твердого тела |
| Скорость поступательного движения |
| Мгновенные движения твердого тела |
| Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела |
