Вращение тела вокруг неподвижной оси
Вращением тела вокруг неподвижной оси называется такое движение, при котором можно указать у тела хотя бы две точки, всё время остающиеся неподвижными.
Прямая, проведённая через эти точки, является осью вращения, неподвижной осью. Этой оси задаётся направление стрелкой (рис. 9.2).
Положение тела вполне определяется углом поворота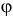 
вокруг оси. Этот угол измеряется в радианах. Чтобы определить положение тела в любой момент времени, должен быть задан угол поворота как функция времени 
.
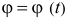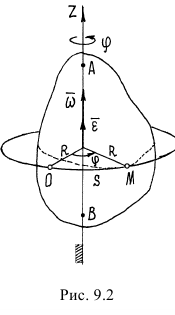
Эта функция называется уравнением вращения тела.
Если в данный момент времени угол 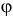положительный 
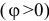, то он откладывается против часовой стрелки. При этом надо смотреть на тело со стороны стрелки оси.
Конечно, траектории всех точек тела -окружности, так как расстояния от точек до оси всё время остаются неизменными. Эти окружности расположены в плоскостях, перпендикулярных оси.
Поскольку траектории точек известны, то можно задать движение точек естественным способом. Закон движения точки по траектории, по окружности, получится таким
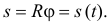
Пусть за время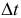 
угол изменился на 
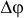. Тогда отношение их будет характеризовать скорость вращения. Эта величина
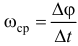называется средней угловой скоростью тела. Конечно, чем меньше 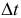, тем точнее будет определена эта скорость. Поэтому точное значение угловой скорости
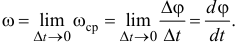
Следовательно, угловая скорость есть первая производная по времени от уравнения вращения, от угла поворота
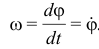
Единица измерения угловой скорости — радианы в секунду. Так как радиан безразмерная величина, то обозначают просто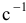 
. В технике скорость вращения часто определяют числом оборотов в минуту 
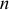. Зависимость между этими единицами измерения: 
.
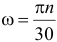Если в данный момент времени окажется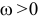 
, то это будет означать, что вращение происходит против часовой стрелки (если смотреть на тело со стороны стрелки оси). Угловая скорость указывает направление вращения тела.
Угловую скорость можно изобразить вектором со, отложенным по оси вращения из какой-нибудь точки в такую сторону, что, если смотреть с его конца, увидим вращение тела против часовой стрелки (рис. 9.2).
Пусть за время 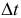угловая скорость изменилась на величину 
.
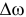Тогда отношение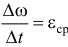 
будет определять среднее ускорение вращения, угловое ускорение. Точным значением его будет предел среднего при
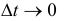
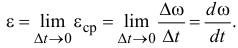
Угловое ускорение есть первая производная от угловой скорости или вторая производная от угла поворота по времени
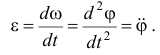
Угловое ускорение также изображают вектором, отложенным по оси вращения. Направление вектора определяется знаком (+) или (-) величины ускорения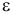 
в данный момент времени.
Комбинация знаков угловой скорости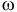 
и углового ускорения 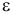определяет характер движения тела. Если их знаки одинаковы, тело вращается ускоренно. Если разные — замедленно.
Так, при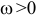 
и 
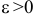тело вращается против часовой стрелки ускоренно. Пр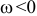и 
и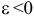 
— по часовой стрелке ускоренно. Пр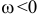и 
и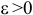 
— по часовой стрелке замедленно. Пр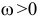и 
и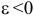 
— против часовой стрелки замедленно.
Поскольку движение точек вращающегося тела задано естественным способом, то нетрудно найти скорости этих точек. Например, скорость точки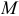 
(рис. 9.3)
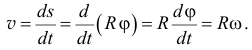
Направлен вектор скорости по касательной к траектории, к окружности, то есть перпендикулярно её радиусу, в сторону вращения.
Используя правило определения векторного произведения двух векторов, можно доказать, что вектор скорости точки
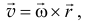
есть векторное произведение вектора угловой скорости со на радиус-вектор точки, которое, действительно, совпадает с вектором скорости и по направлению, и по модулю
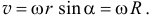
Ускорение точки тела, см. формулу (8.6),
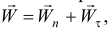
где нормальное ускорение
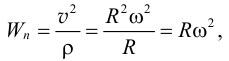
а касательное
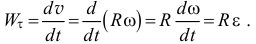
Направляющие векторы этих двух ускорений соответственно по нормали, то есть по радиусу окружности, к оси и по касательной к окружности в соответствии с направлением углового ускорения .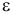
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Ускорение точки |
| Поступательное движение тела |
| Вращение тела вокруг неподвижной точки |
| Плоскопараллельное движение твердого тела |
