Оглавление:
Возвратные уравнения
Уравнения вида
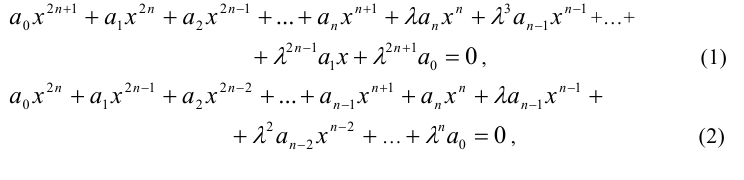
где 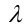 — фиксированное число и
— фиксированное число и 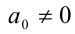 , называются возвратными уравнениями соответственно нечётной и чётной степеней. При
, называются возвратными уравнениями соответственно нечётной и чётной степеней. При 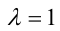 уравнения (1) и (2) являются, в частности, симметрическими уравнениями соответственно нечётной и чётной степеней, при
уравнения (1) и (2) являются, в частности, симметрическими уравнениями соответственно нечётной и чётной степеней, при 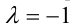 — кососимметрическими.
— кососимметрическими.
Возвратное уравнение нечётной степени (1) всегда имеет корень 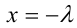 , поскольку это уравнение можно переписать в виде
, поскольку это уравнение можно переписать в виде
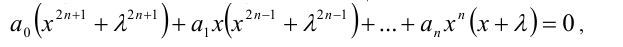
и при 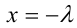 выражения в каждой скобке обращаются в нуль. Выделив множитель
выражения в каждой скобке обращаются в нуль. Выделив множитель 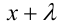 из каждой скобки, можно доказать, что уравнение (1) равносильно совокупности двух уравнений: уравнения
из каждой скобки, можно доказать, что уравнение (1) равносильно совокупности двух уравнений: уравнения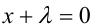 и некоторого возвратного уравнения чётной степени.
и некоторого возвратного уравнения чётной степени.
Для решения возвратного уравнения чётной степени (2) поступают следующим образом. Поскольку x = 0 не является корнем уравнения, то, разделив уравнение (2) на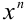 и сгруппировав члены, получим уравнение
и сгруппировав члены, получим уравнение
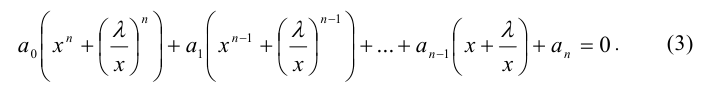
Положим 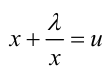 , тогда имеем
, тогда имеем 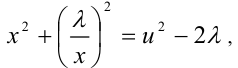
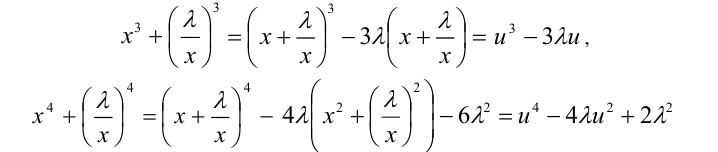
и т.д., и уравнение (3) степени 2n относительно x в результате такой замены преобразуется к виду алгебраического уравнения степени n относительно и . Таким образом, степень уравнения стала ниже в два раза. Если теперь удастся решить полученное уравнение степени n , то тогда можно будет найти все решения уравнения (2).
Пример №192.
Решить уравнение 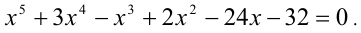
Решение:
Заметим при внимательном анализе структуры уравнения, что его можно переписать в виде
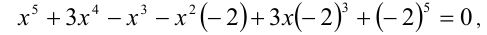
откуда следует, что данное уравнение относится к возвратным уравнениям степени 5 (при 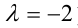 ). Так как согласно теории x = 2 является его корнем, то, сгруппировав члены уравнения, приведём уравнение к виду
). Так как согласно теории x = 2 является его корнем, то, сгруппировав члены уравнения, приведём уравнение к виду
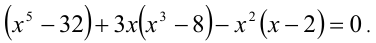
Применяя формулы разности пятых и третьих степеней и выделяя множитель (х — 2), преобразуем уравнение к виду
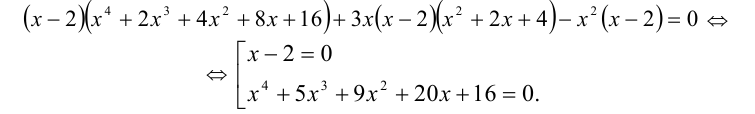
Второе из уравнений совокупности является возвратным уравнением четвертой степени с 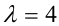 , поскольку его можно переписать в виде
, поскольку его можно переписать в виде
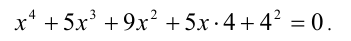
Так как x = 0, очевидно, не является корнем последнего уравнения, то, поделив его на 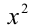 и сгруппировав члены, получим равносильное уравнение
и сгруппировав члены, получим равносильное уравнение
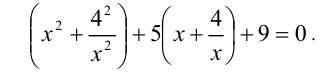
Сделав замену x + (4/х) = и , приходим к квадратному уравнению
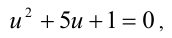
имеющему корни
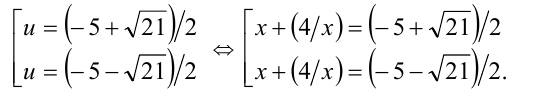
Первое из этих уравнений решений не имеет, второе имеет два корня 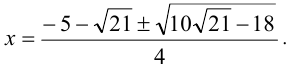 Объединяя решения, приходим к ответу.
Объединяя решения, приходим к ответу.
Ответ: 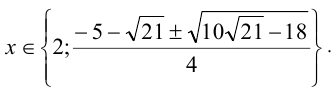
10.Уравнения вида 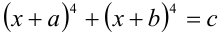 , где а,b,c — заданные числа, отличные от нуля, решаются с помощью замены неизвестной, произведённой по формуле у = x + (а + b)/2 , приводящей уравнение к симметричному виду, в результате чего решение уравнения 4-й степени общего вида оказывается сведено к решению биквадратного уравнения.
, где а,b,c — заданные числа, отличные от нуля, решаются с помощью замены неизвестной, произведённой по формуле у = x + (а + b)/2 , приводящей уравнение к симметричному виду, в результате чего решение уравнения 4-й степени общего вида оказывается сведено к решению биквадратного уравнения.
Пример №193.
Решить уравнение 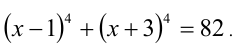
Решение:
Положим 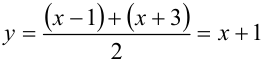 (симметризирую-щая подстановка), тогда уравнение приведётся к более удобному симметричному виду
(симметризирую-щая подстановка), тогда уравнение приведётся к более удобному симметричному виду
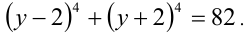
Применяя формулу сокращенного умножения
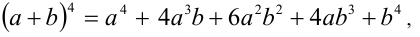
получаем биквадратное уравнение 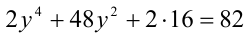 . Поскольку корни квадратного уравнения
. Поскольку корни квадратного уравнения 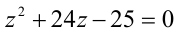 есть
есть 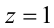 и
и 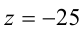 , то находим
, то находим 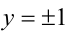 и, следовательно,
и, следовательно, 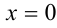 и
и 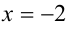
Ответ: 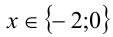 .
.
11.Уравнения вида (х — a)(х — b)(x — с)(х — d) = А , где a<b<c<d , b-a = d- c, 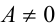
. Для решения уравнения сгруппируем вначале сомножители попарно:
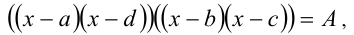
или
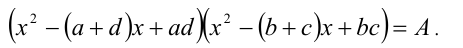
Так как а + d = b + c, то выполним после этого симметризирующую подстановку 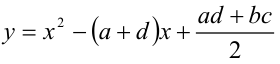 , в результате чего получим уравнение
, в результате чего получим уравнение
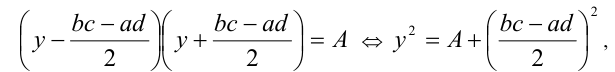
откуда (при условии неотрицательности правой части) находим 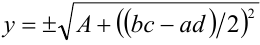 и, возвращаясь к первоначальной переменной, сводим задачу к решению двух квадратных уравнений:
и, возвращаясь к первоначальной переменной, сводим задачу к решению двух квадратных уравнений:
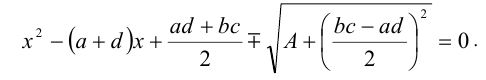
Замечание. Любое уравнение этого вида можно решать иначе, а именно с помощью симметризирующей подстановки
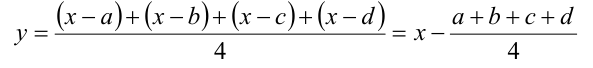
сводить к биквадратному уравнению
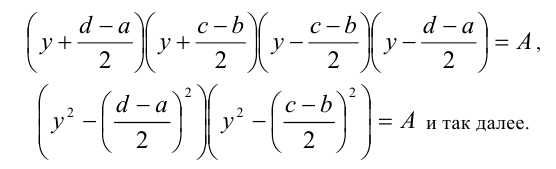
Пример №194.
Решить уравнение
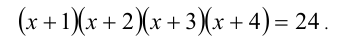
Решение:
1-й способ. Перепишем уравнение в виде: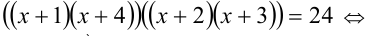
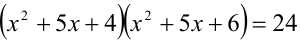 . Обозначим
. Обозначим 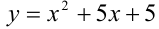 , тогда
, тогда 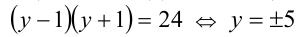 . Следовательно, осталось решить два квадратных уравнения
. Следовательно, осталось решить два квадратных уравнения 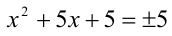 . Одно из них даёт корни x = 0 и x = — 5 , а другое не имеет решений.
. Одно из них даёт корни x = 0 и x = — 5 , а другое не имеет решений.
2-й способ. Сделаем подстановку 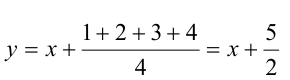 , тогда:
, тогда:
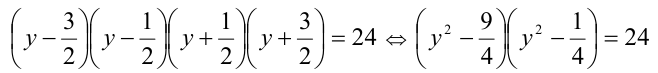
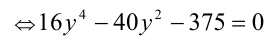 . При этом дискриминант
. При этом дискриминант 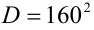 , и единственный положительный корень
, и единственный положительный корень 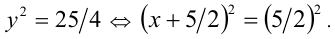 Отсюда приходим к тому же ответу.
Отсюда приходим к тому же ответу.
12.Уравнения вида 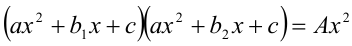 , где
, где 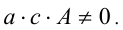
Уравнение этого вида не имеет корня x = 0, поэтому, разделив его на 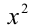 , получим равносильное ему уравнение
, получим равносильное ему уравнение
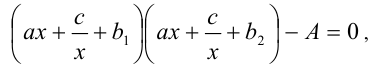
которое после замены неизвестной 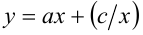 преобразуется в квадратное уравнение, решение которого не представляет трудностей.
преобразуется в квадратное уравнение, решение которого не представляет трудностей.
Пример №195.
Решить уравнение 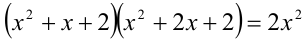
Решение:
Так как x = 0 не является корнем уравнения, то, разделив его на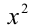 , получим уравнение
, получим уравнение
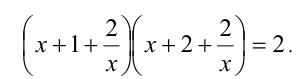
Делая замену у = x + (2/х), получим квадратное уравнение (y + 1)(y + 2) =2 , которое имеет два корня у = 0, у = — 3 . Следовательно, исходное уравнение равносильно совокупности уравнений
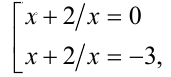
решая которую находим корни. Ответ: 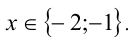
12.Уравнения вида 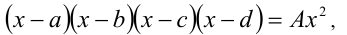 где
где 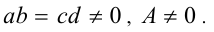 Для решения уравнения такого типа вначале преобразуем его:
Для решения уравнения такого типа вначале преобразуем его:
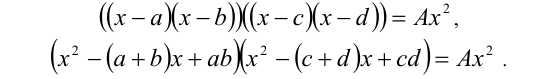
Разделив далее обе части уравнения на 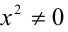 , получим уравнение
, получим уравнение
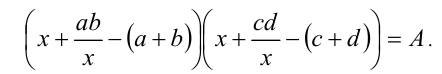
Так как ab = cd , то, выполнив замену 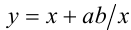 , приходим к квадратному уравнению
, приходим к квадратному уравнению 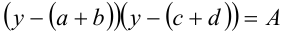 и так далее.
и так далее.
Пример №196.
Выберите промежуток, содержащий сумму всех корней уравнения 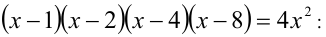 А) (0,6); Б) (6, 12); В) (l 2,18); Г) (18,24); Д) ответы А) — Г) — неверные.
А) (0,6); Б) (6, 12); В) (l 2,18); Г) (18,24); Д) ответы А) — Г) — неверные.
Решение:
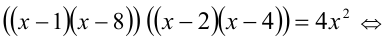
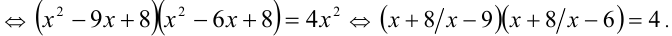
Положим y = x + (8/х), тогда (y — 9)(у- 6)=4. Можно обозначить далее z = у — 7, тогда (z — 2)(z + 1) = 4 <=> z = -2 или z=3. Делая обратную подстановку, приходим к квадратному уравнению 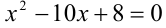 , для которого по теореме Виета находим
, для которого по теореме Виета находим 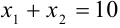 (действительные корни есть, так как дискриминант положителен). Поскольку
(действительные корни есть, так как дискриминант положителен). Поскольку 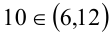 . то, следовательно, правильный ответ будет Б).
. то, следовательно, правильный ответ будет Б).
14. Уравнения вида 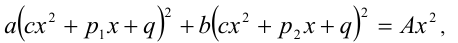 где
где 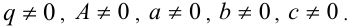
Рассмотрим метод решения такого рода уравнений. Так как x = 0 не является корнем уравнения, то поделим его на 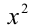 :
:
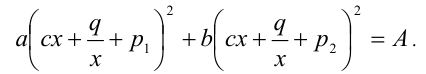
После замены у = cx + (q/x) уравнение приводится к виду квадратного относительно у .
Пример №197.
Решить уравнение
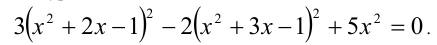
Решение:
Поскольку 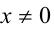 , то уравнение равносильно следующему уравнению
, то уравнение равносильно следующему уравнению
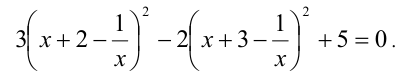
Обозначим 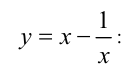
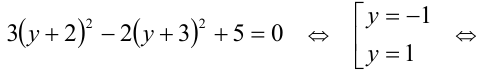
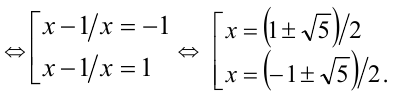
Ответ: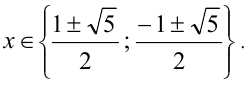
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

