Оглавление:
Возведение в степень
Как уже было показано выше, с целью избавления от модуля бывает эффективен приём возведения в чётную степень, чаще всего в квадрат. Приём обычно используется в ситуации, когда хотя бы с одной стороны от знака равенства (неравенства) находится модуль некоторого выражения, т.е. при решении задач вида
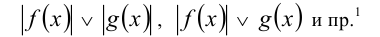
Именно возведением в квадрат проще всего доказывается справедливость при всех действительных x,у известных неравенств
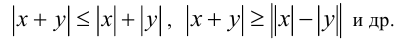
Даже простейшее неравенство вида 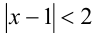 в принципе можно решать возведением в квадрат:
в принципе можно решать возведением в квадрат:
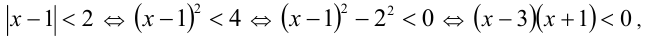
и далее, скажем, методом интервалов. Но обычно сразу переходят к двойному неравенству 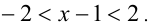
При использовании данного приёма, как правило, следят за тем, чтобы обе части возводимого в чётную степень уравнения (неравенства) были неотрицательны. Это необходимо для сохранения равносильности преобразования. Возможен и переход к следствию, но только в тех случаях, когда можно сделать проверку.
Пример №314.
Найти наименьшее целое число x, удовлетворяющее неравенству
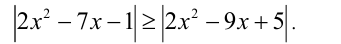
Решение:
Возведём неравенство в квадрат. Так как обе его части были неотрицательны, то получим неравенство, равносильное исходному. Затем, собрав оба слагаемых слева от знака неравенства, разложим левую часть полученного неравенства на множители (как разность квадратов):
1 Знак  заменяет любой из знаков равенства или неравенства.
заменяет любой из знаков равенства или неравенства.
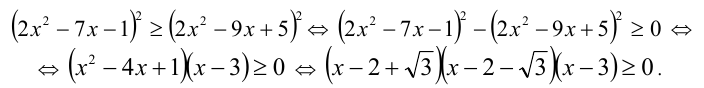
Методом интервалов получаем решения:
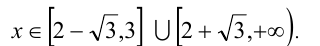
Ответ: наименьшее целое x, удовлетворяющее неравенству, есть 1.
Пример №315.
Решить уравнение
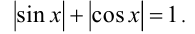
Решение:
Возведём уравнение в квадрат (равносильное преобразование, так как обе части возводимого в квадрат уравнения неотрицательны
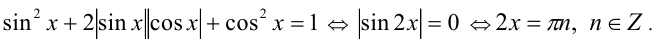
Ответ: 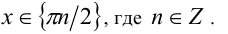
Пример №316.
Решить уравнение
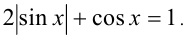
Решение:
Приведём уравнение к виду 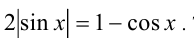 Так как обе части
Так как обе части
полученного уравнения неотрицательны, то возведём в квадрат и придём к равносильному уравнению:
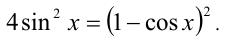
Заменяя в левой части 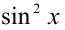 на
на 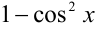 , получаем уравнение, квадратное относительно
, получаем уравнение, квадратное относительно 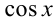 :
:
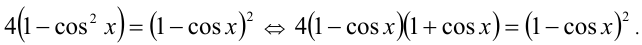
Таким образом, уравнение раскладывается на множители, и приходим к совокупности уравнений:
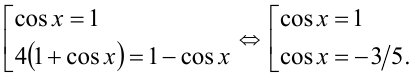
Ответ: 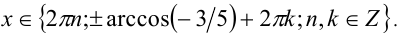
Пример №317.
Решить уравнение
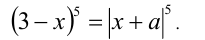
Решение:
Извлекая корень пятой степени (возводя в степень 1/5), получим равносильное уравнение
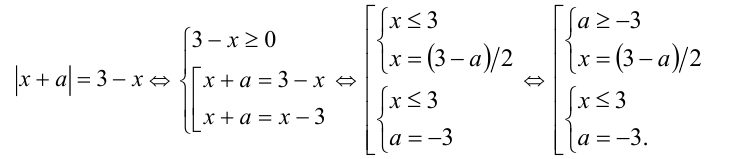
Первая система не имеет решений 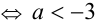 , вторая система не имеет решений
, вторая система не имеет решений 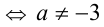 . Обе системы неразрешимы
. Обе системы неразрешимы 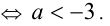
Ответ: наибольшее целое а равно — 4.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

