Возрастание и убывание функции

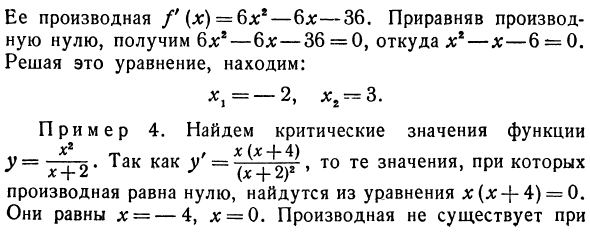
Возрастание и убывание функции

• Функция увеличения / уменьшения Функция определения f (x) называется приращением в сегменте, если значения независимых переменных x1 и x2, полученные в этом сегменте, всегда соответствуют условию от xx , x \ / (*,) для значений независимых переменных x2 и x2, полученных в этом сегменте, интервал a ^ x ^ b Вызывается для уменьшения. То есть, если большее значение независимой переменной соответствует нижнему значению функции, функция называется убывающей. Очевидно Когда функция уменьшается, чем меньше значение независимой переменной, тем больше значение функции (Рисунок 52).

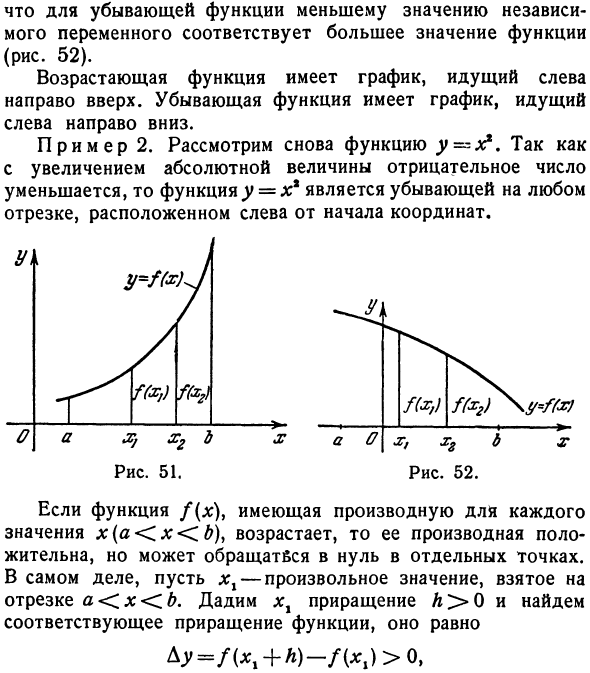
Функция увеличения имеет график, который идет слева направо и вверх. У нисходящей функции есть график, который идет слева направо. Пример 2. . Y, y = f (x) J A *,) f (x2) \ l / = ffxj Оах7хгbхаОx, хгb x Рисунок 51. Рисунок 52. По мере увеличения функции f (x) с производной от каждого значения x (a <.x <.B)> производная становится положительной, но может исчезать в разных точках. Фактически, пусть xx будет любым значением, полученным с интервалом a 0 и найдите соответствующее приращение функции.

Рассмотрим функцию еще раз По мере увеличения абсолютного значения отрицательные числа уменьшаются, а функция y = x1 уменьшается в любом интервале слева от начала координат Людмила Фирмаль

Потому что функция увеличивается. Однако, если вы укажете отрицательное приращение h <C 0 для xx, приращение функции Dy = / (dsr + H) — / (η ^ СО), то есть функция увеличивается, что делает ее отрицательной. Таким образом, для возрастающей функции приращение независимой переменной и приращение функции Всегда один и тот же знак. Таким образом, дробь f + Поскольку он всегда положительный, его предел (значение производной при x = xv) равен положительному или нулю.

Если функция f (x) уменьшается с интервалом a ^ x ^ b и существует производная для каждого значения x, производная для каждого значения x является отрицательной или равной нулю. Для убывающей функции это знак приращения функции и приращения независимой переменной. Фракция — ^ — всегда, потому что это всегда наоборот Из-за знака минус предел равен отрицательному или нулю. Теперь давайте рассмотрим, что можно сказать о функции, когда знак производной известен. производная f (x) — дробный предел ——— ЖЖ h —► ().

• Таким образом, если производная не равна нулю, , f (x + h) -f (x) Достаточно маленький знак n совпадает со знаком ——— LL-L (См. Главу VI, § 4, свойство 5.) Так что если / ‘(х)> 0, То есть f (x + h) -f (x) и h имеют один и тот же знак. Функциональность в этом случае увеличится. f ‘U) <0, f (x + h) h «f (x) кроватка, т.е. знак f (x + h) — f (x) и h разные. Функциональность в этом случае снижена. Эти два последних предложения очень важны в будущих курсах. Значение независимой переменной с нулем или без определенной производной f (jc) называется критическим значением. Пример 3. Поиск важных значений для функции f (x) = 2×3-Back: 1-36L:

Его производная f (x) = 6l; 2-6l: -36. Приравнивая производную к нулю, получим 6l: 2-6l; -36 = 0, почему l; 2-x — 6 = 0. Решение этого уравнения дает: x j = -2, xz = 3. Пример 4. Нахождение критического значения функции x2 „x (ds + 4) y-Y = (x + 2) 2 ak и их значения как 1> Производная равна нулю и может быть получена из уравнения l: (l: +4) = 0. Они равны х = -4, л. = 0 Следующая производная не существует

Поскольку значение xy, в котором исчезает знаменатель, то есть (x; +2) 2 = 0 и x = -2, рассматриваемая функция имеет следующие важные значения: -4, х ± = -2, Людмила Фирмаль

В будущем часто будет необходимо использовать следующие важные характеристики: При пересечении нуля или прерывании могут происходить знаковые переходы произвольной величины (рис. 53). Так, например, значение функции y = 3x — 6 при x = 1 равно 3-1-6 = -3, а значение η = 3 равно 3-3-6 = 3, т.е. эта функция меняет знак , Должен пройти ноль из-за указанного свойства ( Это непрерывно). На самом деле, если x = 2, он равен нулю. Функция y — y со значением x = -1 равна -1, l; = 4 принимает значение ~. Основываясь на этом свойстве, от -1 до 4, можно утверждать, что функция исчезает или прерывается. На самом деле, разрыв происходит, когда х = 0. Это означает, что производные могут менять знак только в том случае, если они передают значимые значения. 0. Рисунок 53.

Смотрите также:

Предмет высшая математика

Простейшие применения производной	Исследование функций на возрастание и убывание
Вторая производная. Производные высших порядков	Максимальные и минимальные значения функции