Оглавление:






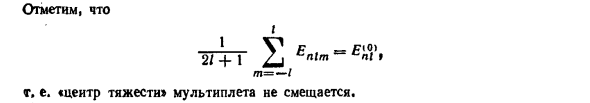

Возмущения, не зависящие от времени
- Возмущения, не зависящие от времени. Точное решение уравнения Шредингера можно найти Тем не менее, только относительно небольшое количество простых случаев. Большинство задач в квантовой механике Сложные уравнения, которые не могут быть точно решены Метод.
Однако во многих случаях, в контексте проблемы, Звание различных орденов. Среди них маленькие светодиоды После игнорирования рейтинга и упрощения задач Точное решение возможно. такой Первые шаги для решения физических проблем Кай состоит из точного решения упрощенной задачи, второй В приблизительном расчете поправки, потому что она мала Член упал с упрощенной задачей.
Гамильтониан заданной физической системы У нас есть форма Людмила Фирмаль
Общий метод Расчет этих поправок называется теорией возмущений. H = H0 + V, Где V — небольшая поправка (возмущение) для «нет». Запутался «Оператор Hq. В §38, 39, Зависящее от времени возмущение V (то же Кроме того, нет также предполагается.
Необходимые условия Оператор V есть «По сравнению с оператором Hq это объясняется ниже. Задача теории возмущений для дискретного спектра Мо. Это можно сформулировать следующим образом: предположение В результате собственная функция φ ^ и собственное значение Известен оператор Hq, то есть известно точное решение уравнения NYA Nof (0) = -E (0) ^ (0). (38,1)
- Необходимо найти приближенное решение уравнения Hf = (Ho + Y) φ = Eph, (38,2) То есть собственная функция φn и Ep значение оператора возмущения N В этом разделе все Различные значения оператора H $ не вырождены. также Чтобы упростить вывод, сначала Дискретный спектр энергетических уровней.
Удобно выполнять расчет с начала матрицы Номинальный формат. Для этого раскройте нужную функцию φ в функции / (0) Ф = ^ 2 St’F (m> — (38-3) T Подставляя это разложение в (38.2) E s ™ (E ™ + = E т т Умножьте это равенство с обеих сторон и интегрируйте Вы найдете (E-E ^) k = ^ 2 ykgpst- (38,4) T Здесь мы вводим матрицу Vkm определенного оператора возмущения V. Ф $ \ делится на невозмущенную функцию vkm = J ^ V ^ dq. (38,5)
Согласно функции мы предполагаем Людмила Фирмаль
Найдите значение коэффициента ct и энергии E в следующем формате ранг E = H (°) + E W + E (2) + …, ct = + c $ + …, Где количество E ^ 1 \ так же мало, как В разделе V величина E ^ 2 \ c $ — это второй порядок и т. Д. Определить модификацию n-го собственного значения, , =, c® = 0, t f p. Чтобы найти первое приближение, В уравнении (38.4), удерживая E = E ^ + En \ s-k-4 ° ^ + c ^ \ Только члены первого порядка.
Уравнение для k = n 4 1} = Vnn = J№ * v№dq. (38,6) Поэтому соответствующая коррекция первого приближения B и др. (Z) j равны среднему значению состояния нарушения f ‘и inlo) p J. Уравнение (38.4) и k f p (1) _ УКП «К к р (°) _p (°)’ ^^ n, (38,7) Cn ^ остается произвольным, поэтому вам нужно выбрать его Функция φη = правильно нормирована До первого члена заказа. Это требует поло Live cn ^ = 0.
На самом деле, функция th 11 = 7ЈP-C / n ‘J- ^ число m <38-8) (Простое число всего символа Поскольку необходимо опустить член m = n), чтобы быть ортогональным к φ®, I / (°). Я (1) 12 Чаша из \ φn + φn \ отличается от единицы только малым значением второго порядка. Уравнение (38.8) определяет поправку первого приближения Для волновой функции.
Тогда, кстати, понятно, в каких условиях Применимость рассматриваемого метода. Должен иметь Место неравенства | ymn | «| 4 °) -j4 °) |, (38,9) То есть матричный элемент возмущения По сравнению с соответствующей разницей в невозмущении Энергетический уровень. Также определите корректировку для второго приближения соответствующим образом. E ^ \ вместо этого значения (38,4) E = E ^ + , G (1), e i (2) (0), (1), (2) +
Рассмотрим Bn + bn, cb = ck + ck ^ ~ ck и второй член В порядке возрастания. Уравнение для k = n E (2) 0 _ ^ ‘y (1) n p- /; vnm L «m> T I38-! «) т р ч (38,7) и Оператор Эрмита V: Vmn = V * n Откуда J! ptL / p L / yy (Заменено с (38.7) на cЈ} Модификация второго приближения к нор Минимальное состояние всегда отрицательно. Конечно, Btr (0) n J соответствует минимальному значению и всем слагаемым в сумме я (38.10) отрицательно.
Кроме того, приблизительные значения могут быть рассчитаны таким же образом. Метод. Полученные результаты обобщаются непосредственно Для оператора Hq с непрерывной спецификацией tra (а мы до сих пор говорим о возмущении Дискретный спектр). Для этого вам нужно только количество дис Добавьте соответствующий интеграл к определенному спектру Непрерывный спектр.
Различают разные состояния Непрерывный спектр с индексом v, работающим непрерывно Набор значений. Что такое V Достаточное значение, чтобы полностью определить состояние (Если состояние непрерывного спектра вырождено, оно почти Это всегда происходит, и недостаточно просто распределять энергию 1) определить состояние).
Тогда, например, вместо (38,8) Должен написать f-] = + 1 ^ (3 8 ‘n) То же самое относится и к другим выражениям. Также полезно дать формулу возмущения Матричный элемент / любой физической величины, Рассчитать до первого заказа с помощью Из функции φn = φф + Φη <c (38,8).
Легко получить Следующая формула: ___ я т т дж? (0) ___ / т г х (0) Ј_ / (0) I \ l V n k J I \ l VkmJnfc / оо-iо \ От Jnm до Jnm «r F (o) _„ (o) F (o) _ F (o) * п к ^ F f p для первой суммы и f t для второй суммы. Задача 1. Определить поправку для второго приближения собственной функции Вы. Решения. Коэффициент (cfp) рассчитывается по уравнению (38.4) C до f p записано в квадратичных терминах cient c! 2)
Функция φη = φ ^ + φ ^ + φ ^ Второй порядок нормализуется. В результате pF) 0 (, нмВннВ) 0 (j нкВк мВ) 2 (I (°) -__ / П / тI | 2 \ Vr Vn-2 ^ 2- ^ * 2 ,,,, Z_ ^ fc2, 2 V ™ 9 Z_ ^ fc2 от м до ж пкш золото ри у нрн з м н ^ н м Где введена частота I W JFt-, A f V / ^? (N °) _ ■ Нет) • P 2. Определить поправку третьего приближения для собственных значений Ням энергии. Решения.
Запишите третий член в уравнении (38.4) с k = n Небольшой заказ, мы получаем 1 7, (3) _ V ^ ‘V ^’ V n m V m k V k n V ^ ‘| K i m | 2 n _ / v / v fe2 ^ nn / v fe2 2 • k m W tpw kp m ™ ^ m n 3. Определить уровень энергии линейных ангармонических колебаний Гамильтониан и ра + ч 2 т 2 Решения. можно получить матричные элементы х3 и х4 Прямо по правилам умножения матриц по формуле Формула для матричного элемента x (23.4).
Для ненулевых матриц X тогда tnemele3 „ (Х) n-3, n- {x) n, n-3 (Х) n -1, n- (X) n, n -1- Поскольку эта матрица не имеет диагональных элементов, она исправлена Аппроксимация из гамильтонова члена ax3 ( Нет помех для гармонического генератора). Коррекция ВТО Аппроксимация от этого члена имеет тот же порядок, что и поправка Идеальное приближение от членов / Зх4. диагональные элементы w4 Иметь форму (X) n, n = (———— ^ • ~ (^ ++++ 1). \ т и / 4
Используя общие формулы (38.6) и (38.10), вы можете видеть, что: Приближенное выражение уровня энергии ангармонической вибрации Закон: c, = bw w ′ („4„ + li) + 5 ^ f-5 −V. V 2/4 N / A J \ 30/2 \ mu J \ 2 / 4. Сферический потенциал с бесконечно высокими стенками Принять форму и претерпеть небольшие деформации (без изменения объема)
Слабый и тонкий эллиптический сфероид с полуосью a = b A. Найти расщепления в уровнях энергии частиц скважины с такими деформациями Мейсонс (А. Б. Мигдаль, 1959). Решения. Граничное уравнение ямы 2, 2 2 W + Y = 1 A2 «г» 2 секунды Изменяя переменные x-> ax / R,> ay / R, z —Y cz / R Сферное уравнение с радиусом .R: x2 + y2 + z2 = такая же замена для .R2 Гамильтона Тониан частицы Н = р2 / 2М = –h2A / 2M (М-масса частицы; энергия (Считая от дна ямы) преобразуется в H = #o + V. H0 = -A, 2 метра V = — час 2 метра * -1 A2 DX2 DN2 + ^ -1 2 1 дз2
Следовательно, проблема эллипсоидальных движений приводит к проблемам О движении в сферической яме. Когда эллипсоид почти такой же, как сфера Для радиуса R = (a2c) 1 // 3 V можно считать малым возмущением. Введите «Эллиптичность» f3 (\ f3 \ 1) : Представляет оператор возмущения в виде V = — @ — (p2-3f z). 3 метра
В первом порядке теории возмущений изменение уровня энергии частицы, По сравнению с уровнем сферической ямы: AEnim = Enim-E $ = (nlm \ V \ nlm) (/ А η — импульс частицы и проекция на ось эллипсоида. Количество уровней данных / сферических скважин. конец т Не зависит). Обратите внимание, что выражение p 2-3 p 2 является zz-compo Неприводимый тензор (тензор с нулевым следом) 5ikp 2-3PiPk,
Согласно (107.2) и (107.6) матричные элементы (nlm \ V \ nlm) pro Пропорционально (-1) t [_ t q w) (■ nlm \ V \ nlm> = (l- ^) (nL | V | n0) (Таблица из 3 ^ символов на стр. 530). Напиши дальше (Nl0 \ v \ nl0) = — / 3E ^ + / 3 ^ nU дг2 ПУ) = м дз (В первом члене уравнение Шредингера р д-р = E (nl0) Для сферических скважин и интеграции со второй частью производится).
О дифференцировании функций фпю = Rni (r) Yio (6, (p) (28.11) формат формулы Yio, d -fpU = (потому что в ~ ——- Оз вор ; в в \ = , (! + 4 (K, -S, i) l l Bl0 + [4 (7 + I) 2-1] 1/2 и [4 / 2-1] 1/2 Радиационный интеграл рассчитывается по формуле Oh Oh Oh J RniR’nirdr = J Rnidr, Ах ах О корка J R’nir2dr = -1 (1 + 1) J Rh dr, Ах ах
Интегрируйте детали и используйте радиальные Уравнение Шредингера (33,3) p «| 2„ // 1 (1 + 1) p _ 2M (o) P n1 n ——— J ^ nl ——————- o ——— L n 1 —— —— TG- nl • г р р Термины с интегралами от R2п1 в ответе отменяют друг друга результат D-E’p / ha-4/3 / (/ + 1) (21-1) (2 / + 3) Пожалуйста, обратите внимание 21 Enlm- + 1 Дж ! _ / (/ + 1) с -Е (0) л (0) т = -1 Другими словами, «центр тяжести» мультиплета не смещается.
Смотрите также:
| Движение в кулоновом поле (сферические координаты) | Секулярное уравнение в физике |
| Движение в кулоновом поле (параболические координаты) | Возмущения, зависящие от времени |

