Возможные перемещения системы. Число степеней свободы
Возможным (или виртуальным) перемещением материальной точки называется бесконечно малое перемещение этой точки, допускаемое в данный момент наложенными на нее связями (без нарушения этих связей).
Возможные перемещения точки нельзя смешивать с ее действительным перемещением. В случае стационарных связей (т. е. связей, не зависящих от времени) действительное перемещение точки есть одно из ее возможных перемещений. Так, если точка лежит на плоскости, то ее возможными перемещениями являются бесконечно малые перемещения в любом направлении по этой плоскости. Действительным же перемещением точки может быть лишь одно из этих возможных перемещений, именно то, которое обусловлено не только характером связи, по и действующими на точку силами и начальными условиями ее движения.
Возможное перемещение точки принято обозначать символом 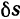 , в отличие от ее действительного элементарного перемещения
, в отличие от ее действительного элементарного перемещения 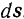 .
.
Возможным перемещением системы называется такое перемещение системы, которое определяется возможными перемещениями ее точек в данный момент.
Так, например, для кривошипно-шатунного механизма (рис. 235) возможным перемещением является такое его бесконечно малое перемещение, при котором вал  кривошипа
кривошипа  поворачивается па бесконечно малый угол
поворачивается па бесконечно малый угол 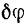 . При этом благодаря наложенным на систему определенным связям все точки механизма также получают соответствующие бесконечно малые перемещения. Возможными перемещениями точек поступательно движущегося ползуна
. При этом благодаря наложенным на систему определенным связям все точки механизма также получают соответствующие бесконечно малые перемещения. Возможными перемещениями точек поступательно движущегося ползуна 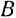 могут быть лишь бесконечно малые перемещения этих точек параллельно неподвижным направляющим ползуна. Возможными перемещениями точек шатуна
могут быть лишь бесконечно малые перемещения этих точек параллельно неподвижным направляющим ползуна. Возможными перемещениями точек шатуна 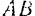 могут быть лишь бесконечно малые перемещения этих точек, которые отвечают соответствующему бесконечно малому плоскому перемещению шатуна.
могут быть лишь бесконечно малые перемещения этих точек, которые отвечают соответствующему бесконечно малому плоскому перемещению шатуна.
Иные перемещения звеньев и точек кривошипно-шатунного механизма (например, поступательное перемещение кривошипа или перемещение ползуна поперек направляющих) наложенными на нею связями (без их разрушения) не допускаются
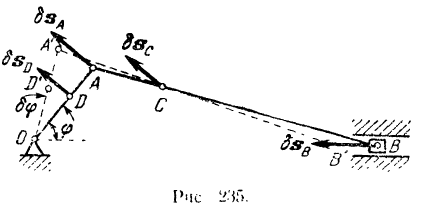
Поскольку под возможными перемещениями понимают не всякие перемещении точек системы, допускаемые наложенными на нее связями, а лишь бесконечна малые, то криволинейные перемещения точек (например, точек 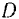 и
и 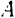 кривошипа
кривошипа 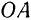 по дугам соответствующих окружностей) можно заменить прямолинейными перемещении направленными по касательным к траекториям этих точек.
по дугам соответствующих окружностей) можно заменить прямолинейными перемещении направленными по касательным к траекториям этих точек.
Возможные перемещения точек несвободной системы ограничены наложенными на нее связями, и потому определения положения точек системы нет необходимости знать координаты всех точек.
Так, например, положение всех точек кривошипно-шатунного механизма вполне определяется заданием только одного угла 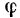 поворота кривошипа. Следовательно, координаты всех точек кривошнпно-шатунного механизма могут быть выражены в функции от одной независимой переменной (угла
поворота кривошипа. Следовательно, координаты всех точек кривошнпно-шатунного механизма могут быть выражены в функции от одной независимой переменной (угла 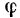 ). Систему, положение которой вполне определяется заданием одной независимой величины, называют системой с одной степенью свободы.
). Систему, положение которой вполне определяется заданием одной независимой величины, называют системой с одной степенью свободы.
Для определения положения в пространстве точек центробежного регулятора (рис. 236) нужно знать уже две величины; угол 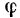 поворота вертикальной оси регулятора и угол
поворота вертикальной оси регулятора и угол 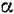 , образованный одним из его стержней (
, образованный одним из его стержней (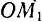 или
или 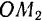 ) с вертикальной осью. Центробежный регулятор имеет две степени свободы.
) с вертикальной осью. Центробежный регулятор имеет две степени свободы.
Независимые координаты, заданием которых вполне определяется положение всех точек данной системы, называются обобщенными координатами этой системы.
Число обобщенных координат системы называется числом ее степеней свободы.
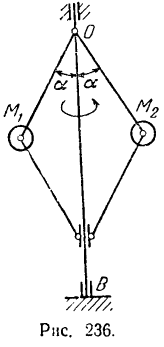
Если положение всех точек системы определяется заданием 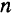 независимых величин (обобщенных координат), то такая система имеет
независимых величин (обобщенных координат), то такая система имеет 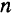 степеней свободы. Так, например, положение точек твердого тела, вращающегося вокруг неподвижной оси, вполне определяется одной обобщенной координатой — углом
степеней свободы. Так, например, положение точек твердого тела, вращающегося вокруг неподвижной оси, вполне определяется одной обобщенной координатой — углом 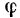 поворота тела, и поэтому такое тело имеет одну степень свободы. Свободная материальная точка имеет три степени свободы, гак как се положение в пространстве определяется тремя, независимыми друг от друга координатами.
поворота тела, и поэтому такое тело имеет одну степень свободы. Свободная материальная точка имеет три степени свободы, гак как се положение в пространстве определяется тремя, независимыми друг от друга координатами.
Число независимых между собой возможных перемещений системы определяет число ее степеней свободы.
Так, например, для центробежного регулятора возможны два независимых друг от друга перемещения: поворот на бесконечно малый угол 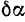 стержня относительно оси регулятора и поворот на бесконечно малый угол
стержня относительно оси регулятора и поворот на бесконечно малый угол 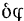 самой оси регулятора. Любое возможное перемещение регулятора может быть составлено из этих двух ею независимых возможных перемещений. Следовательно. центробежный регулятор имеет две степени свободы.
самой оси регулятора. Любое возможное перемещение регулятора может быть составлено из этих двух ею независимых возможных перемещений. Следовательно. центробежный регулятор имеет две степени свободы.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

