Возможные перемещения. Классификация связей
Рассмотрим возможные перемещения точки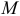 
на стержне, прикрепленном к неподвижной поверхности шарниром 
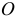(рис. 17.1,а). Конечно, стержень позволяет точке двигаться по сферической поверхности в любом направлении и на любое расстояние. Все эти перемещения возможны. Возможно, кстати, перемещение и вниз. Но такое перемещение не стоит называть возможным, потому что нарушается связь, стержень.
Кроме того, возможным перемещением будем называть только малое перемещение, настолько малую часть траектории, что ее можно заменить прямой, отрезком касательной.
Теперь можно сформулировать определение возможного перемещения.
Возможным перемещением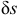 
точки материальной системы будем называть ее бесконечно малое перемещение, допускаемое связями этой системы и без нарушения этих связей.
К этому определению следует добавить несколько замечаний.
Первое. Само название таких перемещений показывает, что они только возможны, но не обязательны; что этих перемещений из данного положения системы может быть много; что среди них только одно есть действительное*; что эти перемещения происходят не под действием сил, приложенных к системе, а, так сказать, по нашему желанию.
Второе. За счет малости таких перемещений направляются они по касательной к траектории и имеют, таким образом, направление, совпадающее с вектором скорости. Эту скорость в данном случае также называют возможной скоростью, а не действительной.
Третье. При наличии связей между точками материальной системы возможные перемещения этих точек связаны между собой определенными зависимостями, уравнениями связей.
На рис. 17.1 дано несколько примеров возможных перемещений точек некоторых материальных систем. Из этих примеров следует, что возможным перемещением всего тела, вращающегося вокруг оси, является малый угол поворота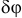 
. И возможные перемещения точек его можно определить с помощью этого угла. Так, например,
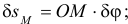
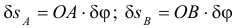
Так как направления возможных перемещений имеют направления скоростей, то перемещения точек звена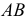 
(рис. 17.1, в) определяются с помощью мгновенного центра скоростей 
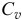этого звена. А возможное перемещение всего тела при плоскопараллельном движении есть поворот на малый угол 
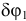вокруг оси, проходящей через мгновенный центр скоростей. Этот угол можно определить.
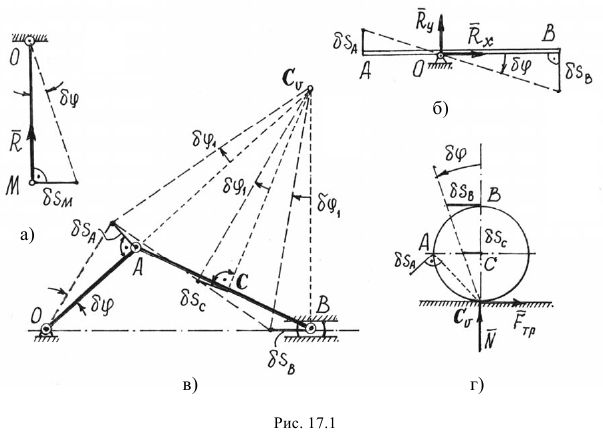
Так как
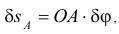
то
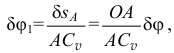
а перемещение ползуна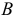 
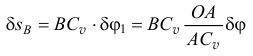
и точки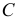 
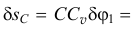
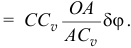
То есть перемещения всех точек этого механизма можно выразить через одно возможное перемещение, перемещение звена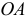 
через угол .
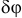Аналогично поворотом на малый угол 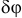вокруг мгновенного центра скоростей 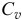определяются возможные перемещения точек колеса, которое может катиться без скольжения по неподвижной прямой (рис. 17.2, г).
Работу сил, приложенных к материальной системе, на возможном перемещении будем называть возможной работой.
Если рассмотреть различные типы материальных систем, можно обнаружить, что элементарная работа реакций многих связей на возможном перемещении окажется равной нулю. Такие связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями. К таким связям относятся, например, все связи без трения. Кстати, об этом сказано было еще в XV, §4.
Связи, которые не изменяются со временем, называются стационарными.
Есть связи, которые называют или удерживающими, или односторонними в зависимости от того, препятствуют они перемещению точки во взаимно противоположных направлениях или только в одном.
У некоторых материальных систем встречаются и довольно сложные связи, ограничивающие или только положение системы, координаты ее точек, или еще и скорость их, производные от координат по времени. Первые называют голономными, геометрическими, связями; вторые — неголоном-ными, кинематическими, неинтегрируемыми. Мы в дальнейшем будем рассматривать системы только с голономными связями.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Принцип Даламбера |
| Силы инерции твердого тела в теоретической механике |
| Принцип возможных перемещений при равновесии материальной системы |
| Принцип возможных перемещений при движении материальной системы |
