Оглавление:



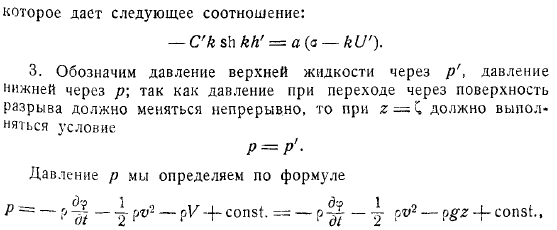




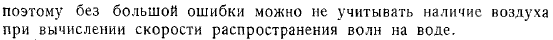

Волны на поверхности раздела двух жидкостей
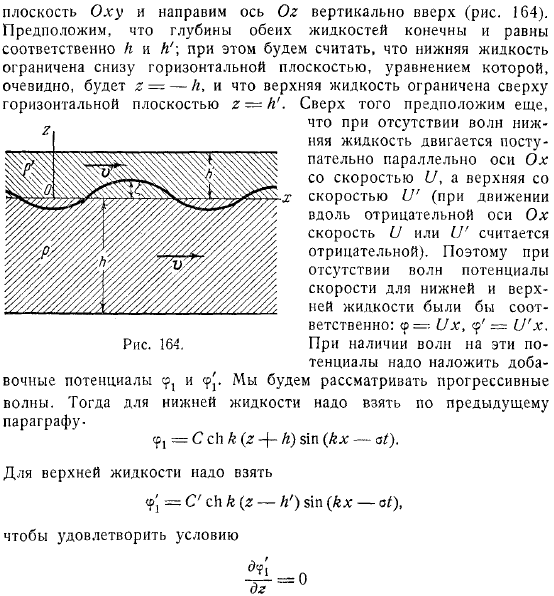
В этом разделе мы рассмотрим теорию плоских волн гидромеханики, которые возникают, когда гравитация действует на границе раздела между жидкостями разной плотности. Плотность нижней жидкости равна плотности верхней. Если обе жидкости находятся в равновесии, граница будет представлять собой горизонтальную плоскость.
Мы полетим на этом самолете. Направьте ось строго вверх. Предполагая, что глубины обеих жидкостей конечны и равны, соответственно, нижняя жидкость при конечной глубине жидкости ограничена снизу горизонтальной плоскостью, уравнение, очевидно, предполагается таким, а верхняя жидкость ограничена сверху горизонтальной плоскостью.
- Дополнение, пока нет. При отсутствии волн нижняя жидкость движется постепенно со скоростью, параллельной оси, а верхняя движется постепенно со скоростью (если она движется вдоль отрицательной оси, скорость считается отрицательной).
- Так, если волн нет, то потенциал скорости нижней и верхней жидкости будет соответственно.
Если есть волны, то к этим потенциалам необходимо приложить дополнительные потенциалы. Людмила Фирмаль
Рассмотрим бегущие волны. Затем, для более низкой жидкости, она должна быть принята согласно предыдущему пункту.
Верхняя жидкость должна быть взята для удовлетворения условий. Поэтому рассмотрим волны определенной длины. Поэтому на данный момент сумма остается. Необходимо определить из следующих условий. Давайте посмотрим на некоторые частицы нижней жидкости, которые находятся вблизи самого уравнения, на саму границу раздела.
- Поскольку рассматриваемая частица всегда будет примыкать к границе раздела, ее координаты всегда будут заполнены. Просто письменное уравнение.
- Таким образом, вертикальная проекция скоростей рассматриваемых частиц имеет вид. Но частица имеет горизонтальную скорость, основной частью которой является. Или получить следующее окончательное условие.
На самом деле, это условие должно быть выполнено при получении вышеуказанных условий, потому что оно учитывает только минимальную волну и игнорирует минимум высшей. В этом случае наиболее естественно взять межфазное уравнение (см. Предыдущий абзац
Вы можете легко получить, вычисляя и подставляя для найденного уравнения. Людмила Фирмаль
Если учесть частицы верхней жидкости, которые капиллярные волны расположены вблизи поверхности зазора, то получим условие вы получаете следующие отношения. Обозначим давление верхней жидкости, давление нижней жидкости, поскольку давление при прохождении через поверхность трещины должно непрерывно изменяться.
И условия должны быть выполнены. Давление определяется по формуле. В нашем случае вы можете игнорировать последний термин, включая бесконечно малый размер. Член с конца, его можно заменить расчетом на. Это связано с тем, что данный термин уже содержит коэффициент минимального значения.
Такая же ситуация возникает и в расчетах. Поэтому вычислить таким же образом. Уравняйте эти выражения, чтобы получить. To к этому добавим ранее полученные формулы. Возвращает уравнение для определения, за исключением. Поскольку мы нашли это уравнение из предыдущего уравнения, мы определяем его, чтобы полностью решить проблему.
Скорость распространения полученной волны, как обычно, определяется уравнением. Поэтому, вводя его в предыдущее уравнение вместо его значения, вы получите уравнение, которое поможет вам решить левая сторона всегда положительна. Это указывает на наличие волны рассматриваемого нами типа, только если легкая жидкость находится выше тяжелой.
В противном случае амплитуда малейшего возмущения значительно возрастет. То есть, основное движение обеих жидкостей становится неустойчивым. Однако даже в некоторых длинах волн основное движение становится неустойчивым. Для простоты мы предполагаем, что обе жидкости очень глубоки, так что они приемлемы.
Уравнение, определяющее c, принимает вид. Вы можете решить это легко. Чтобы быть материальными, радикальные выражения должны быть позитивными. Это приводит к неравенству. Если поток не тот же самый, то есть большой поток, что это неравенство не выполняется.
Однако большой короткой длине волны соответствует, поэтому основное движение становится неустойчивым к малому. Дело в том, что при малой длине волны следует также учитывать действие капиллярной силы (см. Следующий абзац), которая действует на стабилизацию, обеспечивая устойчивость основного движения, в котором нет столь больших различий. Следует отметить, что в более конкретных случаях, то есть когда нет течения, скорость распространения длины волны определяется по формуле.
Если вы получаете знакомое выражение. Для водных и воздушных систем, потому что плотность воды в несколько раз выше плотности воздуха. Именно поэтому, не совершая большой ошибки, можно игнорировать наличие скорости распространения волн на поверхности воды при расчете.

