Пример решения задачи №25.
Во сколько раз надо изменить скорость тела, брошенного горизонтально, чтобы при вдвое большей высоте, с которой оно брошено, получить прежнюю дальность полета? Сопротивлением воздуха пренебречь.
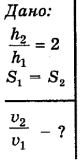
Обозначим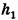 
высоту, с которой бросили тело в первый раз, 
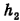— во второй, 
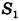— дальность полета тела в первый раз, 
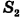— во второй, 
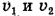— горизонтальные скорости тела в первый и второй раз соответственно.
Решение:
Попытаемся связать в одну формулу скорость, с которой тело брошено горизонтально, высоту броска и дальность полета. Если мы получим такую формулу для первого броска, то, заменив индекс 1 у буквенных величин на индекс 2, мы сможем записать аналогичную формулу применительно ко второму броску, а уже затем найти и отношение скоростей.
Чтобы связать воедино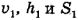 
запишем уравнения движений тела по горизонтали, а затем исключим из этих уравнений время t. По горизонтали тело движется равномерно, поэтому
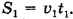
По вертикали тело свободно падает без начальной скорости, так как проекция скорости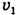 
на ось ОУ, направленную вертикально вниз, при бросании в горизонтальном направлении равна нулю. Поэтому уравнение движения по вертикали с высоты h будет:
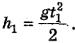
Если теперь выразить время t из формулы (1) и подставить его в формулу (2), мы найдем искомое соотношение скорости, высоты и дальности полета:
Аналогично применительно ко второму броску запишем:
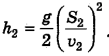
Если теперь разделить (4) на (3), то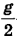 
сократится, а также сократятся и расстояния 
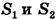, ведь они согласно условию равны друг другу. Тогда из оставшегося выражения мы и определим искомое отношение скоростей
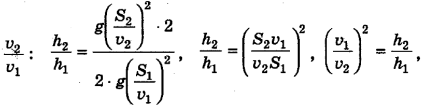
откуда
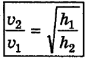
Задача решена. Вычислим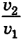 
:
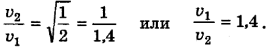
Следовательно, при увеличении высоты вдвое и прежней дальности полета горизонтальную скорость следует уменьшить в 1,4 раза.
Ответ: в 1,4 раза.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
