Оглавление:




Внутренние усилия в сечениях стержня при стеснённом кручении. Гипотезы
- Сдерживание внутренней силы в поперечном сечении стержня с закруткой. Это теория. Как упоминалось выше (§ 67), свободное скручивание стержня в поперечном сечении вблизи контура имеет тангенциальное напряжение, направленное вдоль контура(см. Рисунок). 141§ 67). Поэтому он находится на противоположной стороне прямоугольника или овала, который показан на рисунке. 141, касательное напряжение направлено в разные стороны. При
касательном напряжении распределяется в одном сечении от элементов тонкостенного и чистого кручения стержня Но) лл ( е Ют] 1ЛЛП г) Например, они параллельны контуру и направлены в противоположные стороны(рис. 462). Здесь тангенциальная сила сводится к паре, которая складывается из суммы моментов внутренних сил, как показано на рисунке. 462, г: _ _ = Очевидно, что чем меньше толщина стенок стержня, тем меньше плечи внутренней пары, и, соответственно, тем больше значение касательной’.
Отсюда следует, что чем тоньше стенка скрученного стержня открытого профиля, тем 2) Известия СПб будут сопротивляться даже крутящему Людмила Фирмаль
моменту. 4 и 5,1905-1906§ 173] внутренняя сила стержневой части 533 Есть и другая сторона. Дж Относительно небольшое значение M K в сечении возникает из-за больших касательных напряжений. Также отметим, что тангенциальное напряжение при толщине стенки профиля направлено на(рис. 463), осевая линия сечения должна быть равна нулю. Таким образом, центральная поверхность скрученного стержня также свободна от смещения, а основной прямоугольник, взятый на промежуточной поверхности в любом месте по длине стержня, свободен от скручивания. Теперь перейдем к рассмотрению вопроса о сдержанном (изогнутом) кручении. В дополнение к одному
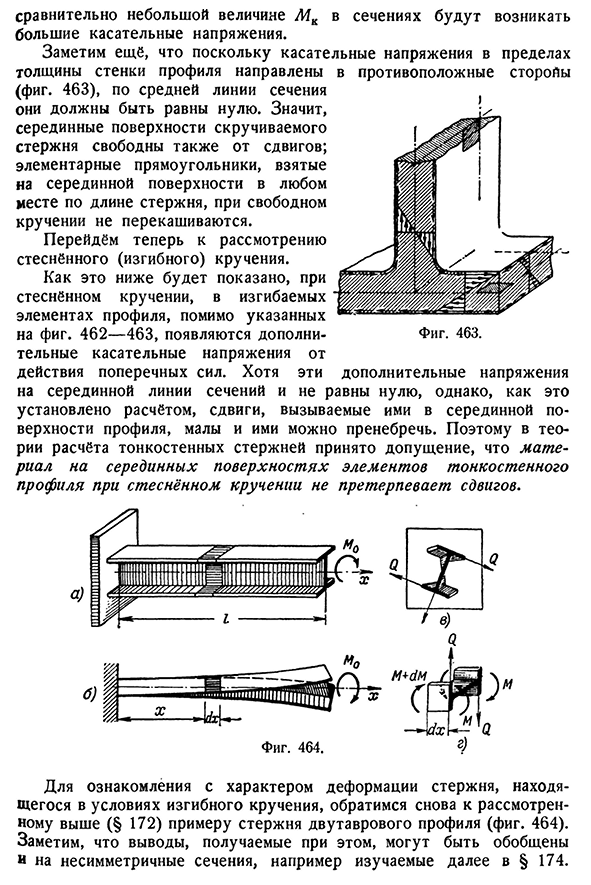
в диаграмме, в изогнутых элементах профиля, под ограниченным кручением, как показано ниже. Существует дополнительное касательное напряжение от действия боковой силы, 462-463. Однако эти дополнительные напряжения на осевой линии сечения не равны нулю, а устанавливаются расчетным путем, поэтому в середине профиля, в теории расчета тонких стержней, предполагается, что промежуточный материал на плоскости тонкостенного сечения при стесненной закрутке не смещается. Для выяснения особенностей деформации сердечника в условиях изгибного кручения мы вновь
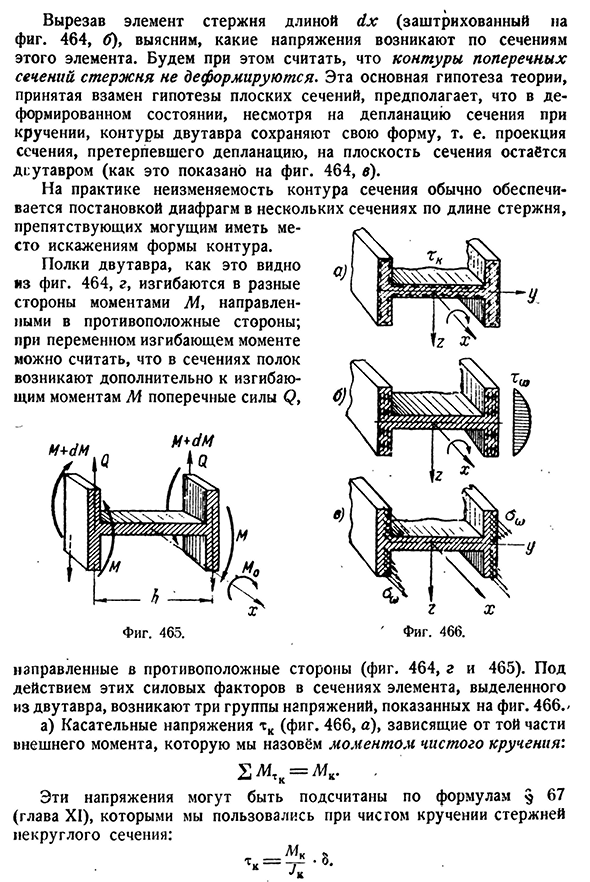
- имеем дело с приведенным выше примером (статья 172) сердечника двутаврового профиля (фиг. 464). Заметим, что выводы, полученные в этом случае могут быть обобщены на асимметричные участки, например, при расчете тонкостенных решеток на основе§ 174.534, и дальнейшие исследования х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х. х Путем разрезания стержневого элемента длиной d x (тень на рисунке. 464, б), посмотрим, какое напряжение возникает в этом разделе элемента. Предположим, что профиль поперечного сечения стержня не деформируется. Эта основная гипотеза теории принята вместо гипотезы плоского поперечного сечения, в деформированном состоянии, несмотря
на отрыв поперечного сечения в твисте, контур двутавровой балки является 464, в). Дело в том, что инвариантность контура сечения обычно обеспечивается установкой диафрагмы в несколько сечений по длине стержня и не возникает. Я луч на полках, как видно на рисунке. 464, g, изгибается в разные стороны моментом W, направленным в противоположные стороны; в переменных изгибающих моментах, помимо изгибающего момента M, действует боковая сила Q в сечении полки., Фигура. 466. Направленный в противоположную сторону(рис. 464, г и 465).
В сечении элемента, изолированного от двутавровой балки, под действием этих силовых факторов возникают три группы напряжений, как показано Людмила Фирмаль
на рисунке. 466, а) касательное напряжение TC(фиг. 466, а) называет моменты чистого крученияв зависимости от той части внешнего момента. Эти напряжения можно рассчитать по формуле 67 (глава XI), которая использовалась для чистого кручения стержня некруглого сечения: Тонна −3§ 173] внутренняя сила поперечного сечения стержня 535 Здесь геометрическая характеристика сечения при кручении условно называется моментом инерции при кручении, а толщина стенки сечения в рассматриваемой точке равна 3; 7К-чистая ne. 466, б). Эти касательные напряжения в рассматриваемом случае можно рассчитать с помощью метода Журавского, когда станет известна величина поперечной силы. Заметим, что сила Q сопряжена с моментом Mia=Qh(рис. В) нормальное давление полок
двутавра; поскольку эти внешние силы приводятся в действие совокупностью внутренних сил (рис.466), образующие статически сбалансированную систему из них пропорциональны относительному удлинению волокон, вызванному неравномерным истощением сечения, называемому нормальным напряжением сечения, обозначенным Ош. Когда участок отслаивается, некоторые волокна становятся длиннее, другие короче, и есть нейтральные волокна, которые не подвергаются ни растяжению, ни сжатию. Изгиб и кручение тонкостенных стержневых деталей не являются
плоскими, поэтому нулевая точка обычно не находится на прямой линии, но нейтральные волокна не группируются в нейтральном слое. Поскольку действие указанных выше трех групп напряжений (t K>и«) эквивалентно действию внешнего момента (MX-M^составьте уравнения равновесия для их определения 466): v y=0,^A W^=0^; (30.1)*£30.1,J * Z=0; (30.2) J dF * M2=0,^d F-y=30.3) V/Y=i7= » —no ^ −0 или l4k — | — l4sh=l4v. (30.4)536 базис[chap. XXX Из шести статических уравнений два являются тождествами(30.1)、(30.2)、(30.3)является условием, что нормальное напряжение(as)сводится к системе внутренних сил, которая полностью уравновешивается. В случае двутаврового изгибного кручения считаем, что система внутренних вертикальных сил, действующих на поперечное сечение полки, сводится к двум парам L4, направленным в противоположные
стороны (465 и 466, в). Такое сочетание двух пар в параллельной плоскости называется гадюкой. Величину гадюки можно оценить по новому коэффициенту силы (квадратичному моменту, равному произведению момента M), расстоянию между ними h (плечо гадюки): B=M-h. Этот новый обобщенный силат) относится к неравномерной деградации сечения и эквивалентен статически уравновешивающей системе внутренних вертикальных сил, называемых Бимодальными изгибами, поэтому вместо нахождения изгибающего момента, приложенного к отдельным элементам скрученного стержня, можно поставить задачу определения величины изгибающего момента бимомента В. Поэтому для расчета касательных и нормальных напряжений в поперечном сечении стержня необходимо найти значения 7IK и V. Приведенные выше
уравнения равновесия (30.1), (30.2) и (30.3), поскольку закон изменения нормального напряжения сектора нам неизвестен и ни один из интегралов не может быть взят, задача определения напряжения в поперечном сечении тонкостенного стержня статически неопределенна. Чтобы решить ее, нужно учитывать упругую деформацию. В рассматриваемом примере сдержанного скручивания стержня двутавровой балки изгибаются только полки двутавровой балки, а осью скручивания стержня является его центральная ось x, причем в несимметричном сечении сечения, или в случае симметричного сечения одноосной балки, вращение сечения
происходит не вокруг центральной оси центра изгиба (в этом случае центром скручивания будет центр кручения). При сдержанном скручивании подобного стержня происходит не только изгиб полки, но и изгиб профильной стенки. Но общий результат вывода можно свести к тому же уравнению(30.1)—(30.4). * ) Понятие «обобщенная сила» переводится как » обобщенное перемещение!»Условие, что обобщенная сила равна 1, равно работе обобщенного перемещения. *) См., например, б у Ч К О В и М р о щ и Н С К и й, скручивание и изгиб металлических балок, стройздат, 1944, с. 64.
Смотрите также:

