Оглавление:


Внутренние силы в стержне и их определение
- Внутренняя сила в стержне И их определения В процессе деформации стержня под нагрузкой взаимное расположение элементарных частиц объекта изменяется, и в результате изменяется внутренняя сила. По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающих целостность и соответствие деформации. Чтобы идентифицировать эти силы, вам
нужно использовать метод сечения: мысленно рассечь стержень в равновесии на две части и одну из них, например, часть B (рис. 12, а) Рассмотрим равновесие. 14 Со стороны выброшенной части на часть В действует система внутренних сил, распределенных по всей секции. В общем, эта система может быть сведена к одной силе
R (главный вектор) и одной паре M (главный момент). При исследовании Людмила Фирмаль
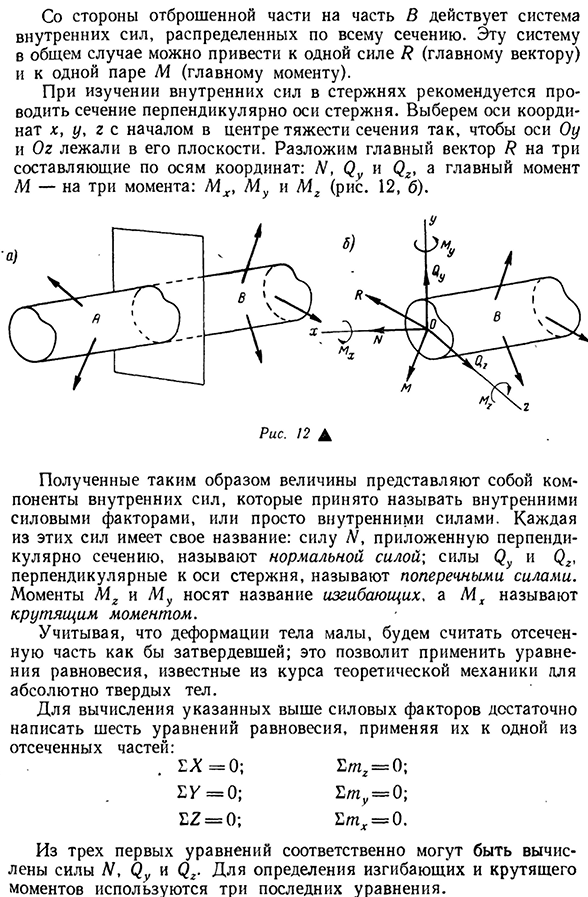
внутренней силы стержня рекомендуется сделать поперечное сечение перпендикулярно оси стержня. Выберите оси координат x, y, r и поместите начало координат в центр тяжести сечения так, чтобы оси Oy и Og находились в этой плоскости. Главный вектор R разлагается вдоль оси координат на три составляющие N, Qy и Qz, а основной момент M- разлагается на три момента M x, My и M z (рис.
12, б). Полученное таким образом значение является компонентом внутренней силы, обычно называемой коэффициентом внутренней силы, или просто внутренней силой. Каждая из этих сил имеет уникальное имя. Сила Л1, приложенная перпендикулярно к поперечному сечению, называется нормальной силой, а силы Qy и Qz, перпендикулярные оси стержня, называются боковыми силами.
- Моменты Mz и My называются изгибающими моментами, а M x называется крутящим моментом. Учитывая, что деформация тела мала, вырезанная часть считается закаленной. Это позволяет применять уравнения равновесия, известные в процессе теоретической механики абсолютных твердых тел. Чтобы рассчитать приведенный выше коэффициент силы, достаточно написать шесть уравнений равновесия и применить их к одному из разрезов. EU = 0; E t y = 0; EZ = 0; Exx = 0. Из первых трех уравнений силы N, Qy и Qz могут
быть рассчитаны соответственно. Последние три уравнения используются для определения изгиба и крутящего момента. Когда к стержню прикладывается сложная нагрузка, все шесть компонентов внутренней силы могут одновременно появляться в поперечном сечении. Что касается сопротивления материала, то изучение поведения стержня под нагрузкой начинается с простейшего случая силового воздействия (рис. 13). Когда внешняя сила, действующая на режущую часть стержня, уменьшается до результирующей силы вдоль оси стержня, в поперечном сечении появляется
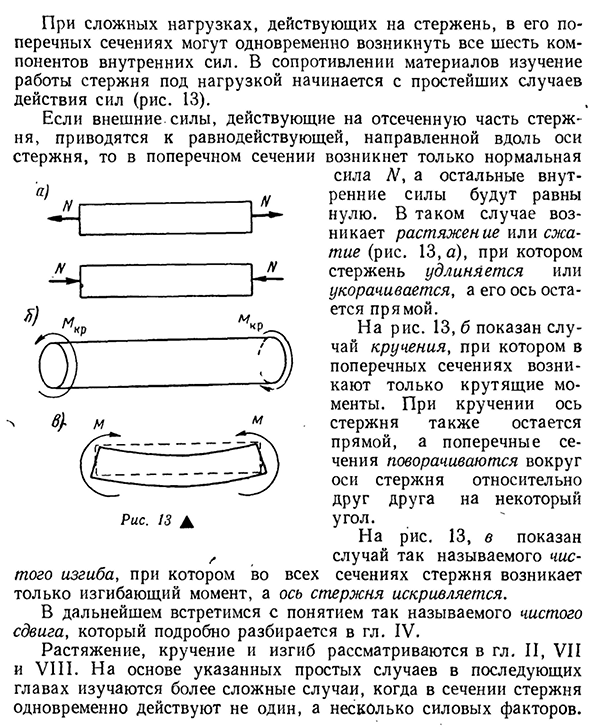
только нормальная сила N, а оставшаяся внутренняя сила становится равной нулю. В этом случае возникает растяжение или сжатие (рис. 13, а), Людмила Фирмаль
стержень расширяется и сжимается, а его ось становится прямой. На фиг.13b показан случай закручивания, когда в поперечном сечении возникает только крутящий момент. Когда стержни скручены по прямой линии, соединения поворачиваются на определенный угол друг относительно друга вокруг оси стержня. Рисунок 13c является так называемым Ось остается, горизонтальная ось Изгиб, при котором все секции стержня испытывают только изгибающие моменты, а ось стержня изогнута. В будущем мы встретимся с концепцией так называемого чистого сдвига. Ч об этом. Внутривенно Растяжение, скручивание и изгиб обсуждаются в разделе 2. II, VII и V III. На основе этих простых случаев в следующих главах будут рассмотрены более сложные случаи, когда на поперечное сечение стержня воздействуют одновременно несколько силовых факторов.
Смотрите также:
| Пример определения секториальных характеристик | Кручение тонкостенных стержней открытого профили |
| Виды нагрузок и схематизация элементов сооружений | Кручение упругих стержней сплошного профиля |

