Оглавление:





Внецентренное сжатие или растяжение.
- Внецентровое сжатие или растяжение. Вторым существенным случаем дополнительной деформации от изгибающих и продольных сил является так называемое внецентровое сжатие или растяжение, вызванное только продольными силами. Этот вид деформации получается при действии двух равных противоположных сил на стержень Р, направленных вдоль прямой, параллельной оси
стержня(рис. 427). Расстояние точки А от центра тяжести сечения около А=Е называется эксцентриситетом. Во-первых, рассмотрим случай внетропического сжатия, который имеет более практическое значение. Наша задача-найти наибольшее напряжение в материале стержня и проверить его прочность
. Для решения этой задачи мы применяем в двух точках, равных 5 0 0, совместное действие изгиба и растяжения или сжатия[гл. XXUP Мощность P (Рис. 428). Людмила Фирмаль
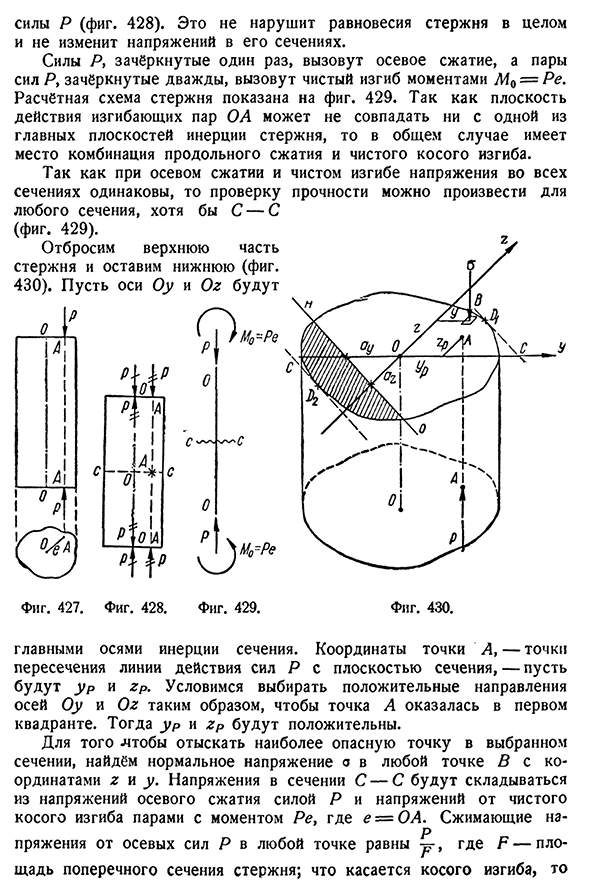
Он не нарушает равновесия всего стержня и не изменяет напряжения в сечении. Сила P вызовет осевое сжатие, как только стирается, а пара сил P вызовет чистый изгибающий момент M$=PE, перечеркнутый дважды. Расчетная схема стержня приведена на рисунке. Поскольку рабочая поверхность 429 изгибающей пары ОА может не совпадать ни с одной из основных поверхностей инерции стержня, в общем
случае имеет место сочетание продольного сжатия и чистого косого изгиба. Осевое сжатие и чистое напряжение изгиба всех секций одинаковы Главная ось инерции секции. На пересечении линий действия силы-координаты точки D, — плоскости пересечения линий силы p и поперечного сечения-P и z P можно выбрать положительное направление оси OU и Oz так, что точка A будет первым квадрантом, тогда ur и z P будут положительными. Чтобы найти наиболее опасную
- точку в выбранном сечении, вы найдете вертикальное напряжение o в любой точке с координатами z и y. сжатие на R Отклонение от осевой силы P в любой точке равно y, F-площадь поперечного сечения стержня; что касается косого изгиба,§ 163] VIECENTRAL сжатия или растяжения 501 Замените его действием изгибающего момента главной плоскости. Изгиб плоскости x OU вокруг нейтральной оси Oz обусловлен моментом Рура, придающим точке B нормальное сжатие-Рур*—g—. ЮЖД Аналогично, является ли нормальное напряжение в точке B, вызванное изгибом в главной
плоскости x Oz, вызванным моментом pzp? * Z и выражается в Формуле — — -. Суммируя напряжение от осевого сжатия и двух плоских изгибов и считая напряжение сжатия отрицательным, получим следующее уравнение для напряжения в точке B: P Ruru P^RG/1\ — в J2.— (27.4) Эта формула подходит для расчета напряжений в любой точке любого поперечного сечения стержня, при этом можно рассчитать координаты точек относительно главной оси вместо y и z в их знаке. Для внецентровых растяжек все компонентные признаки нормального напряжения точки B обращены вспять.
Таким образом, для того чтобы по формуле (27.4) получить правильный знак напряжения как при внецентровом сжатии, так и при внецентровом растяжении, помимо координатных символов y и g, необходимо Людмила Фирмаль
вычислить знак силы P. Там должен быть знак плюс, при сжатии—минус. Полученная формула может придать немного другой вид; Для скобок-давайте посмотрим на множитель p.: Где iz и 1U-радиус инерции сечения относительно главной оси (вспомним Jz-iz-F и Jy=i* — F). Чтобы найти точку максимального напряжения, нужно выбрать y и z так, чтобы a достигло максимального значения. Переменные в формулах (27.4) и (27.5) являются последними двумя членами, которые отражают эффекты изгиба. Причем, как и в случае изгиба, максимальное напряжение получается в самой дальней точке
от нейтральной оси Си, и здесь, как и в случае косого изгиба, необходимо найти положение нейтральной оси[гл.6 0 2 совместные акты сгибания, растяжения или сжатия. XXVII Обозначим координаты точек этой линии через j/0 и g0; так как в точке нейтральной оси нормальное напряжение равно нулю, то после подстановки значений _u0 и G0 в уравнение (27.5、: Или 1 + ^+¥=0. (27.6) Зет Очевидно, мы получили уравнение прямой линии, которая не проходит через центроид сечения. Чтобы построить эту линию, проще всего рассчитать отрезки, вырезанные вдоль оси координат. Покажем эти
отрезки AU и az. Чтобы найти отрезок AU, отрезанный к оси OU, необходимо по формуле (27.6) поставить «г»=0;_uo=АУ\ Тогда мы получаем: 1+^ — ’ = 0 и= Точно так же、 л=0’^ = АГ, Получать: А2= -^ -. (27.8) з п Если значения УР и ZP положительны, то отрезки АС и А2 являются отрицательными. 430). Нейтральная ось делит сечение на две части-сжатие и растяжение; на фиг. 430 растянутый участок-это тень. Подводя к контуру касательную поперечного сечения параллельно нейтральной оси, получим две точки Dx, и там будут максимальные сжимающие и растягивающие напряжения. Измерьте
координаты y и z этих точек, подставив их значения в Формулу (27.4) для вычисления значения максимального напряжения в точке D2: ’(1,2)= — Py+Y -^ -+ материал стержня равномерно растянут (27.10)§ 163] вне центра сжатия или растяжения 503. Для поперечных сечений с выступающими углами, где обе основные инерционные оси являются осями симметрии (прямоугольник, двутавр и др.), поэтому формула (27.10) упрощается, g1^3×1= ^ ^ 4″ ^ + ^ ] (27.11) Если материал стержня не оказывает равномерного сопротивления растяжению и сжатию, необходимо проверить прочность стержня в растянутой
и сжатой зонах. Однако может случиться так, что в таком материале испытание на прочность будет достаточным. Из формул (27.7) и (27.8) видно, что положение точки А и положение нейтральной оси приложения силы взаимосвязаны: чем ближе точка а находится к центру сечения, тем больше ur и gr связаны между собой. Итак, по мере приближения точки А к центру тяжести сечения нейтральная ось удаляется от него, и наоборот. Так, в некоторых положениях точки А нейтральная ось проходит вне секции, и вся секция работает при напряжении одного знака. Очевидно, что в этом случае достаточно постоянно проверять прочность материала в точке
Dv. Рассмотрим существенно важный случай изготовления стержня прямоугольного сечения(рис. 431) приложенная к точке А, смещенная от центра сила Р, лежащая на главной оси поперечного сечения ОП.: г р= — \ — е\ЗП=В. Напряжение в любой точке будет Потому что… -ЭТО НЕМНОГО ШОКИРУЕТ, — СКАЗАЛ ОН. F12M12 ЮЖД~БЧ~Б * 9 Напряжение во всех точках линии, параллельной оси выхлопа, одинаково. Положение нейтральной оси определяется отрезком взлетел=ОО. (27.13) 504 Синергия сгибания, растяжения и сжатия[Глава II. XXVII Нейтральная ось параллельна оси OZ. Точки с наибольшими растягивающими и сжимающими напряжениями расположены на сторонах 1-1 и 3-3. Если вы назначите это значение вместо y в выражении (27.12), вы получите значения atax и amin
Смотрите также:
| Изгиб балки при действии продольных и поперечных сил. | Ядро сечения |
| Учёт деформаций балки | Определение изгибающих и крутящих моментов |

