Оглавление:


Внецентренное растяжение — сжатие
- Расширение Voicefree-сжатие. Назад Следующее уравнение (103.4) применяется к обычным случаям, когда имеется осевая составляющая внешней силы, рассматриваемая в приложении к главной плоскости) __ AlvX F/X Sy с внецентровыми проблемами натяжения или сжатия
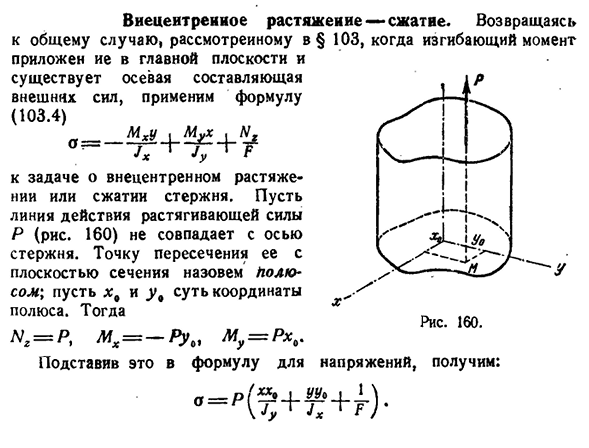
стержня. Давайте попробуем линия действия тяги-напряжение П(фиг. 160) не соответствует оси стержня. Мы называем взаимодействие полюсов с плоскостью сечения, где x in и y in-координаты полюсов. Тогда N Z=P, M x= — R y a, Mu = Px.» Назначить следующее выражение 103, когда изгибающий момент Давление, получаем: 238 давление изгиба[гл. IX Например, J-
это величина с размерностью длины четвертой степени, поэтому ее можно Людмила Фирмаль
выразить следующим образом: здесь имеется определенная величина lianey iy, называемая радиусом инерции. Точно так же Заключительная запись выражения для стресса выглядит следующим образом:+? +1) ’ (и 0L) симметрия этого уравнения относительно переменных x, y и x0, y a доказывает следующую теорему: T e o R e m a1. Напряжение в точке 1, которое вызвано силой, параллельной
оси стержня, через которую линия действия проходит через точку 2, генерируется из той же силы, при которой линия действия проходит через точку 1. Выровнять левую часть до нуля (110.J), получаем уравнение прямой, где точка не напряжена:^+^T! +1=0-(110.2) ’u1X’ Эта линия называется нулевой линией. Напишите выражение в виде
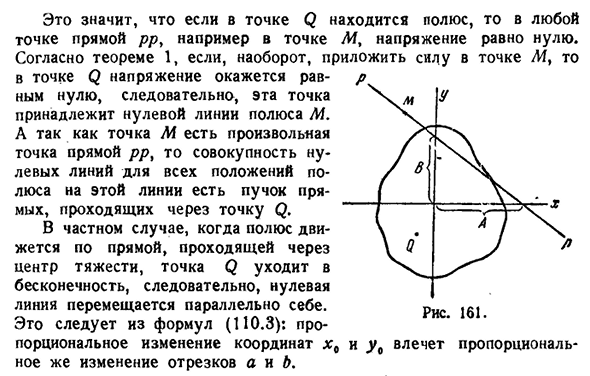
- уравнения для прямой линии в отрезке(110.2):±+£_1=0, а * б’ Куда? Но = — Й=(нет. Зет) Х.} ’Уа — Отрезки, вырезанные нулевой линией на координатных осях, получают простым способом построения нулевой линии: заданными координатами полюсов являются отрезки а и в, через их ребра проводится прямая линия, которая становится нулевой линией. Здесь мы докажем следующую теорему: T e o R e m a2. Когда полюса перемещаются по прямой линии, нулевая линия вращается вокруг неподвижной точки. Пусть PP(рис. 161) есть линия, чтобы сократить линию A и линию B на координатных осях.
Рассмотрим ее как нулевую линию, и в соответствии с формулой (110.3) координаты соответствующих полюсов точки Q являются ядром _I’y% x q — — — — — — — — — — d’*§ 111] раздел 239 Это означает, что если в точке Q имеется полюс, то в точке линии PP, например, в точке M, напряжение согласно теореме 1, наоборот, когда сила приложена к точке Q, напряжение будет равно нулю.
Так как точка M является произвольной точкой линии PP, то множество нулевых линий для Людмила Фирмаль
всех положений полюсов на этой линии представляет собой пучок линий, проходящих через точку Q. В частном случае при движении по прямой, через которую полюса проходят центр тяжести, нулевая линия движется параллельно самой себе, так как точка Q бесконечна. Это следует из Формулы (110.3): пропорциональное изменение координат x0 и y0 есть такое же изменение отрезков a и B.
Смотрите также:
| Несущая способность стержня при изгибе | Ядро сечения |
| Принцип Сен-Венана | Несущая способность внецентренно сжатого стержня |

