Оглавление:


Внецентренное действие продольной силы
- Функционирование внецентрового продольно-направленного усилия Если продольные силы действуют на центр и параллельны продольной оси балки, то балка испытывает сжатие или растяжение в центре. Расстояние от продольной силы до оси балки е называется
С С Е Н Т Р и С и т е т о м к е. пусть пересечение продольной силы и поперечного сечения-полюсов силы-имеют
координаты ur и gr в системе координат главной центральной оси. Приложив Людмила Фирмаль
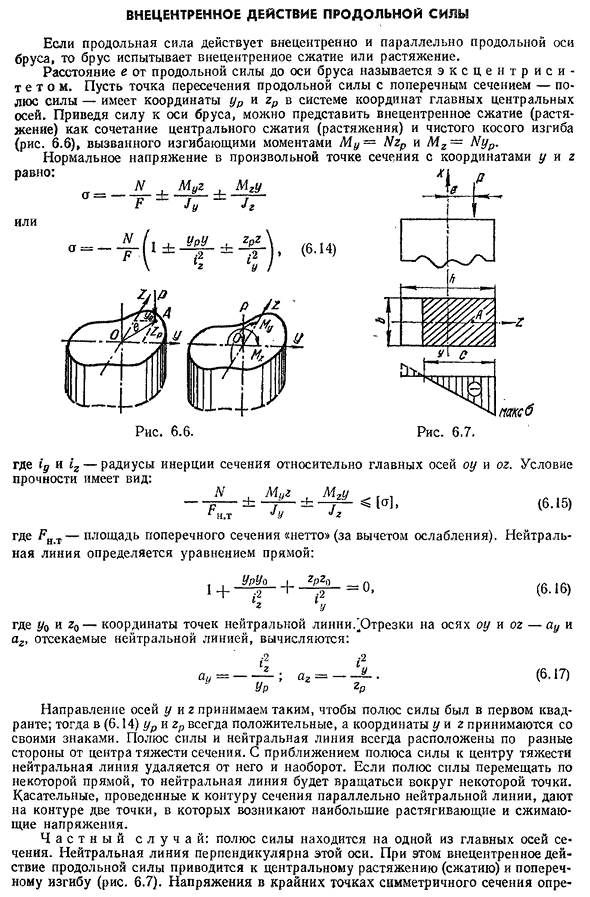
усилие к оси балки, вы можете представить себе центральное сжатие (растяжение) как комбинацию Центрального сжатия (растяжения) и чистого конического изгиба (рис.). 6.6) изгибающий момент обусловлен L4U=Nzp и Mg=Nyp. Нормальные напряжения г————-■» —
—— —— — — ’— ~ •• — -равных: Или Н Mu2 Координаты Y и Z в любой точке поперечного сечения Где IG и iz-радиус инерции сечения относительно главных осей Oh и Oh. Условие имеет следующий вид: Н Fnt Jy[o], (6.15), где FHT-«чистая» площадь поперечного сечения (минус затухание). Нейтральная линия определяется уравнением
- прямой линии: Uluo 1+И2 г РГ о (6.16)) Где y0 и G0-координаты точки нейтральной линии.’Вычислите отрезки осей OU, og-AU и AG, вырезанные нейтральными линиями: •2″2 =»г=—(Б.* 7) Ур Г Р Р Направление оси YG принимается таким, что полюса силы находятся в первом квадранте, тогда в(6.14) ur и gr всегда положительны, а координаты y и g берутся с их знаком. Силовой полюс и нейтральная линия всегда находятся на противоположной
стороне от центра тяжести секции. Когда полюса силы приближаются к центру тяжести, нейтральная линия отделяется от него, и наоборот. При движении по прямой, где расположены полюса силы, нейтральная линия вращается вокруг определенной точки. Касательная, проведенная по контуру поперечного сечения параллельно нейтральной линии, дает контур из двух точек, где присутствуют максимальные растягивающие и сжимающие напряжения. H a S t N s y S l u h A y: силовой стержень
находится с другой стороны на главных осях секции. Нейтральная линия Людмила Фирмаль
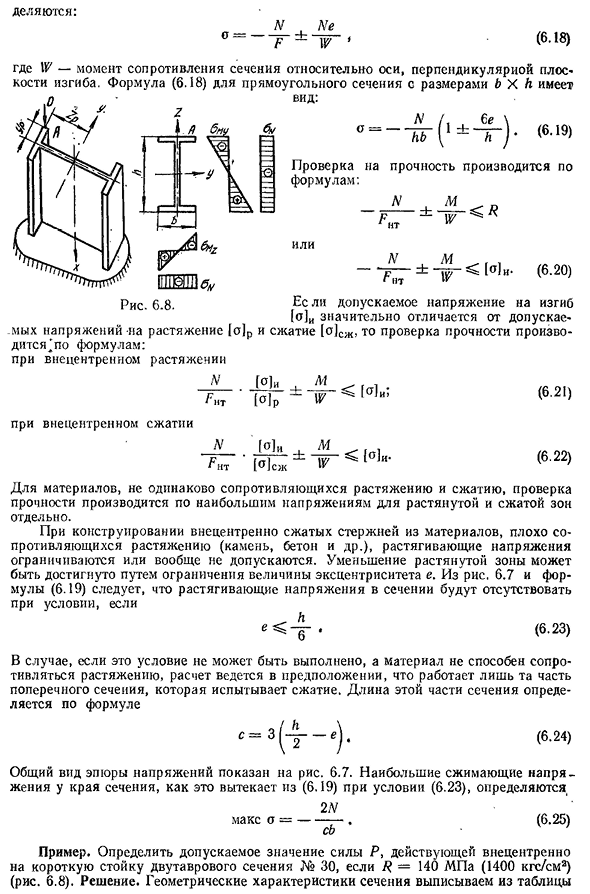
перпендикулярна этой оси. В этом случае действие отклоняющихся от центра продольных сил приводит к центральному растяжению (сжатию) и поперечному изгибу (рисунок). 6.7). Экстремальное точечное давление в симметричном сечении Опре- Шесть.* 163delayutsya: О= Нэ Ф~Ш ’ (6.18) Здесь W-момент сопротивления поперечного сечения относительно оси, перпендикулярной плоскости изгиба. Формула прямоугольного сечения (6.18) с размерами b×h выглядит следующим образом: Или Отчет
Испытание на прочность проводят по формуле: Н F NT Н М, Когда допустимое напряжение на изгиб[o]и допустимое напряжение на растяжение[o]p и сжатие[o]CJ существенно различаются, испытание на прочность проводят по следующей формуле. F NT (6.21) Со сжатием от центра Н F NT (6.22)) Для материалов, которые не одинаково устойчивы к растяжению и сжатию, испытание на прочность проводится отдельно при самом высоком давлении
для растянутых и сжатых зон. При проектировании нецентрированного сжатого стержня из менее стойких материалов (камень, бетон и др.) растянуть.), Напряжение растяжения ограничено или вообще не допускается. Это может быть достигнуто путем изменения размера объекта. 6.7 и уравнение (6.19) растягивающие напряжения в этом разделе будут отсутствовать. * <6-2 3 ) Если это условие не может быть выполнено и материал не может сопротивляться растяжению, то расчет реален в предположении, ч
то только участок участка, который подвергается сжатию работает, длина этого участка определяется по формуле (6.24) На диаграмме показана вся картина этой диаграммы напряжений. 6.7. Максимальное напряжение сжатия на кромке сечения, как следует из(6.19)при условии(6.23), определяется по формуле 2.В Макс о= ——
—, (6.25) ЦБ. Например. Определите допустимое значение силы Р, действующей в случае короткой стойки I-го сечения № 30, р=140мпа (1400кгф/см2) (фиг. 6.8). Решение. Геометрические свойства сечения выписываются из таблицы 164sortamenta: ч-30СМ; б=13.5 см; Ф-46, 5 см2,дя=7080cm4;ЮЖД-337cm4;Вайоминг — =472cm3;ВЗ=49. 9cm3; iv-12,3 см; 12=2,69 см. Координаты полюсов силы A: y=. 6,75 см; ЗП=15см. Внутренние силы постоянны по длине стойки и равны: jV=—P; Mu = RGR; Mg=Ruhr. На рисунке показана фигура нормального напряжения, обусловленного всеми внутренними силами. 6.8 как вы можете
видеть, опасная точка-это точка а, потому что она имеет наибольшее сжимающее напряжение. Запишите условия прочности нормального напряжения(6.14): __ 15 _ P•6 ′ 75 — <1400- 46.5 472 49.9′ 0,188 Р<1400, Из него допустимое значение силы Р определяется величиной 1400 [L R]J s j——— = 7450 кгс или 74,5 КН.
Смотрите также:
| Пространственный косой изгиб | Ядро сечения |
| Совместное действие изгиба и продольной силы | Расчет бруса круглого сечения |

