Оглавление:





Влияние вязкого трения на вынужденные колебания системы с одной степенью свободы
- Второе уравнение Лагранжа в этом случае имеет вид д ДТ ДТ ДП ДФ, Н ты-Д4 Щ 10. Где Т 1-кинетическая энергия системы, а п 1 CQI-потенциальная энергия системы. P 2-диссипативная функция, а Q t — возмущающая сила, функция заданного времени. Если ввести эти значения в уравнение 10 2 Р с, вопрос О 2 4 — 1c 0, 11. Здесь указывается c a A2, p a 2l. Решение дифференциальных уравнений II , если возмущающая сила Q является синусоидальной функцией или может быть выражена в виде ряда Фурье, описано в томе 2, Глава VIII, 4, пункт 4.
Для любой зависимости возмущенной силы от времени решение уравнения H выражается формулой q e-nl ft cos kit 13s sin kit й Г Е-Н стаки т-р ДТ, 12 Где ft и-начальное значение обобщенных координат и обобщенной скорости. УЛ2-Л2-собственная частота системы. Первый член справа определяет свободную вибрацию системы, вызванную начальным отклонением от положения равновесия и сообщением системе начальной скорости Ци-е-и1 футы потому что грех к. 13 2-й член справа от 12 обозначает принудительное перемещение. Система возникает под действием возмущенной силы Q , приложенной к системе. Дж М т е, t и Синай — Т рфт.
Ниже рассматриваются как системы, состоящие из конечного числа материальных точек, так и системы тел с непрерывным распределением масс. Людмила Фирмаль
14. Если эффект возмущения приложен к системе в виде единичного импульса 5 1, который приложен к неподвижной системе в первый момент, то последующие движения происходят по формуле Пятнадцать Функция 15 называется откликом системы на один импульс. Когда постоянная единичная сила Q 1 в первый момент приложена к неподвижной системе, система движется в соответствии с уравнением. 16- Функция 16 называется реакцией системы на единичное возмущение или на переходную проводимость. Для решения задачи вынужденной вибрации системы, учитывающей силу вязкого сопротивления, рекомендуется следующая процедура. 1 Выбрать обобщенные координаты, определяющие отклонение системы от положения равновесия.
2. Создать представление потенциальной и кинетической энергии системы, а также диссипативных функций и выразить их в обобщенных координатах и обобщенной скорости. 3 Создайте малое колебательное дифференциальное уравнение системы, используя уравнение Лагранжа типа 2 4 интегрируем дифференциальные уравнения колебаний и находим уравнение движения системы. Задание 18.21.Устройство для измерения вертикальной вибрации монтируемого корпуса состоит из массы m, которая прикреплена к краю пружины, и ее коэффициента жесткости I — S.
Масса m соединена с жидкостным демпфером и создает силу сопротивления, пропорциональную относительной массе-скорости Esa коэффициент пропорциональности 0.Выше — колебания с уравнением сообщают до конца весны Г ч потому что ПТ. Выпуск 18.21.Частота свободного колебания массы m равна, а коэффициент затухания 0 равен критическому значению l j 2 Если затухающее колебание переходит в апериодическое движение. Определить амплитуду установленных вынужденных относительных колебаний массы относительно рамы, регистрируемых прибором на барабане. Решение. Создайте дифференциальное уравнение для движения груза, вибрируя при этом раму, на которой установлены груз и пружина.
- Используя метод относительной динамики движения, который показывает в r координаты смещения массы относительно корпуса устройства — навигация—Т. 1 Это ускорение точки подвешивания.- Это инерционная полезная нагрузка. После упрощения Р 2У уу-у, 2 Где P ХД 2л, СД к От состояния проблемы — РГ cospA Если ввести это значение в выражение 2 2 2ni A z H cospA 3 Конкретное решение для определения вынужденных колебаний массы выглядит следующим образом Ярл. Л2-Р 4л Р потому что ПТ. 4 В соответствии с условиями величина p 2l — l равна 2 значениям критического спада l j p 2p5ps или k n.
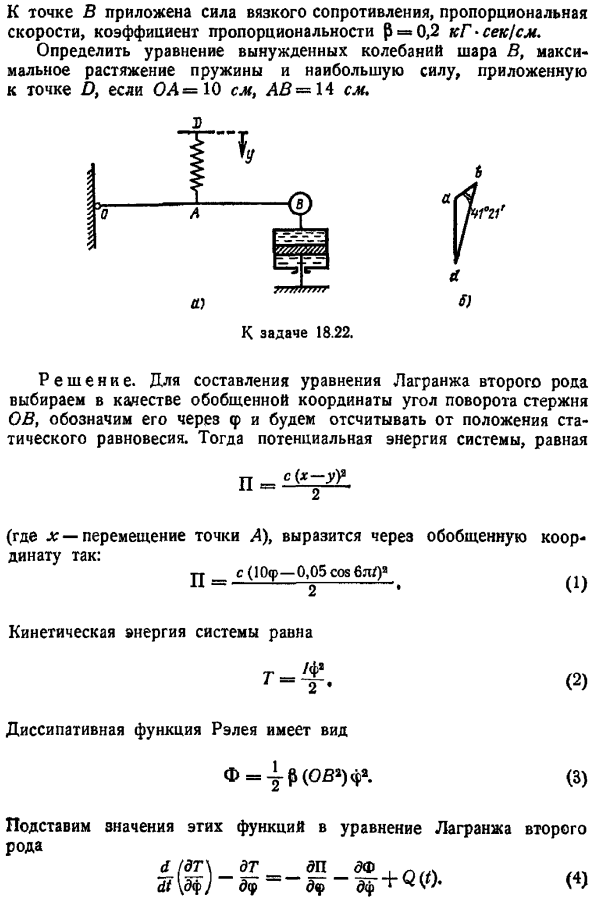
Рассматриваемом вопросе присвоить ему значение l A p2. 4, Найти Амплитуда этих колебаний Пчела Р Задача 18.22.Эта система состоит из штанги OB с прикрепленным шариком B. Стержни поворачиваются в точке O рисунок a .Момент инерции колебательной системы относительно горизонтальной оси через точку О, перпендикулярную фигуре, равен 26,83 кгс-с-с. Пружина крепится к стержню в точке а, коэффициент ее жесткости равен c 120 кг с. 2-й конец пружины D совершает заданную вертикальную вибрацию по формуле Коэффициент вязкостного сопротивления Р 0,2 кг-с см прикладывается к точке В, которая пропорциональна скорости.
Если же рассматривать систему, состоящую из одного первого шара, то давление второго шара па первый является внешней силой. Людмила Фирмаль
Для 04 10 см, для 45 14 см определите уравнение вынужденной вибрации шарика B, максимальное растяжение пружины и максимальное усилие, приложенное к точке D. б Но… Solution. To составьте уравнение Лагранжа 2-го класса, выберите угол поворота стержня OB в обобщенной системе координат, обозначьте его через p и посчитайте с позиции статического равновесия.
Тогда потенциальная энергия системы, равная X-смещение точки А, выражается в обобщенных координатах следующим образом н с 10В −0.05 потому 6л 11 Кинетическая энергия системы Два Форма диссипативной функции Рэлея имеет вид Ф-1р с 4- Подставим значения этих функций в уравнение Лагранжа 2-го порядка О 2 3 Мы узнаем это по порядку с 10 П-0.05 в COS 6л 10 — Вопрос 0-0. Вводя эти значения в 4, можно было бы ф п или 1 Ф 1 OOsf 0,5 С, потому что 6л, 5 Или 26.83 f 0.2 24 f 12 OOOf 60 cos 6l. Разделите обе части уравнения на высшую производную Ф 4.3 ф 447ф 2.24 cos 18.85. Амплитуда вынужденного колебания определяется выражением это определяется l f U L — p 4p P Ф, 2.24 0.018 Радиан.
Уравнение вынужденной вибрации центра шара B выглядит следующим образом ХВ 24 0.018 Кос 18.85 −0.7217, 7 Разность фаз Найдите максимальное натяжение пружины рисунок B .Максимальное смещение верхнего конца пружины D составляет ab 0,05 см. Максимальное смещение нижней кромки пружины в точке С равно bd 10 0.018 0.18 см. Отложите эти сегменты под углом 41 21 разность фаз. Задняя сторона треугольника ad равна максимальному удлинению пружины рис. Б. по косинусной теореме объявление 0.05 0.18 −2.0.05-0.18-cos41o21 0,15 см. Наибольшая мощность точки D Вопрос саd 120-0.
Смотрите также:
Предмет теоретическая механика

