Оглавление:



Влияние включения в модель переменной, которая не должна быть включена
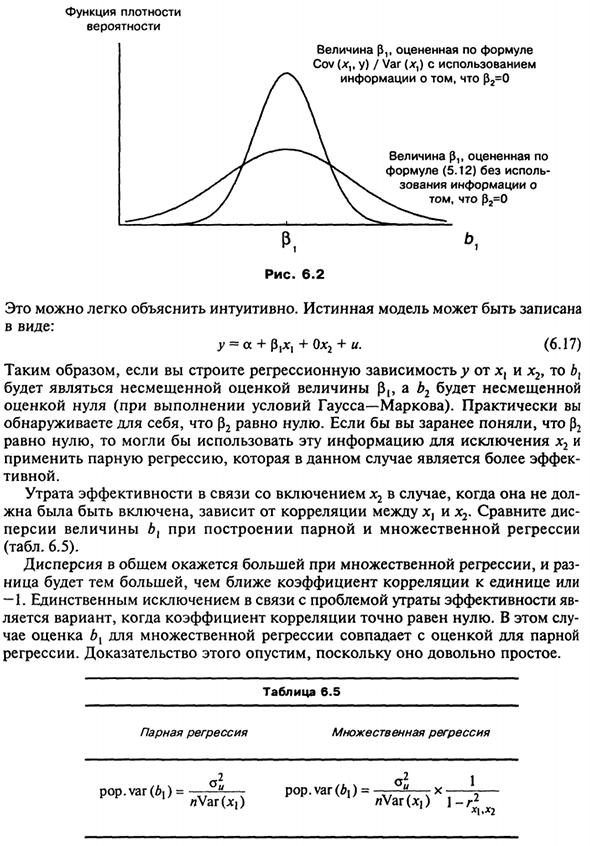
- Эффект включения переменных в модель, Не должны быть включены Предположим, что истинная модель представлена в виде: y = a + p, x, + u, (6.15) А ты y = a + $ {x {np ^ + m, (6.16) Используйте уравнение (5.12) вместо уравнения для расчета оценки Женя Соу (xp значение hL (оценочное значение 51т Без использования формулы y / J ^ v (5.12) yS f \ x. Информация о ^^ / \ ^ ч.
- Дело в том, что p2 = 0 Рисунок 6.2 Это легко и интуитивно понятно. Вы можете записать истинную модель В следующем формате: y ^ a + fiiXt + Oxi + u. (6,17) Так что, если вы строите регрессионную зависимость >> от x и x2, b { Является объективной оценкой значения (5l5 a b2 является непредвзятой Оценка нуля (при условии Гаусса-Маркова). Практически ты Вы можете видеть, что p2 равен нулю. Если вы понимаете p2 заранее.
Если ноль, используйте эту информацию, чтобы получить х2 Применить попарную регрессию. Людмила Фирмаль
В этом случае это более эффективно tivny. В противном случае потеря эффективности при включении х2 В зависимости от соотношения между х и х2, жена была включена. сравнить дис Персидские значения bx при построении парной и множественной регрессии (Таблица 6.5). Дисперсия обычно увеличивается при множественной регрессии и один раз Чем лучше, тем ближе коэффициент корреляции к единице -1.
Единственным исключением из проблемы потери эффективности является Вариант вводится, если коэффициент корреляции точно равен нулю. В этом случае Кроме того, оценочное значение b {для нескольких регрессий, совпадает с оценочным значением пары Регрессия. Поскольку это довольно просто, мы опускаем это доказательство.
Таблица 6.5 Парная регрессия множественная регрессия 2 a 2 j pop.var (A) = 17 «h pop.var (bx) = u x r— «Var (x,) / iVar (x!) 1-r * L |, L 2 178 Есть одно исключение из заключения о необъективности, которую вы должны иметь Имейте в виду. Если x2 коррелирует с и, коэффициент регрессии В конце концов будет предвзятость. Если модель записана в виде уравнения (6.17), это 4-е условие Гаусса-Маркова применяется к х2 не выполняется.
Эксперимент Монте-Карло В эксперименте Монте-Карло, описанном в разделе 6.2, Завышено влияние образования на доход из-за того, что учителя не учитывают Зависимость дохода конкретной страны от значений IQ, Значение 5 было случайно частично использовано в качестве переменной подстановки для IQ. Высоко определенное уравнение парной регрессии.
Имейте это в виду И предположим, что наши исследователи уже являются экспертами в этом Вопросы, приглашенные в качестве аналогичного консультанта Я слежу за своим соседом. В новых странах такой подход может оказаться более формальным, чем первый. Доход здесь определяется только образованием (и удачей) без учета метода Такие, как.
- Где базовый доход снова равен 10000, 2000 плюс (или минус) каждый год в течение как минимум 10 лет исследований Несколько значений в зависимости от коэффициента удачи. Истинное соотношение Это выглядит так: у = 10000 + 2000 (5-10) + и = -1 0 000 + 20005 + и. (6,18) Исследователь снова создаст образец из 20 человек. Все они имеют те же характеристики, что и в первой части. Tab. 5.2. В этом случае есть также данные о значениях IQ.
Верь в это Расчет значений IQ регрессии безвреден, исследователи Выполните эту операцию, чтобы получить следующий коэффициент (стандартная ошибка Ки показано в скобках): у = -1 3 336 + 21405+ 18 / (3 (6,19) (4155) (151) (43) Результат действительно хорош. 95% доверительный интервал Константа содержит истинное значение 10000.
Интервал для S включает значение 2000. Людмила Фирмаль
Следовательно, полученное оценочное значение В отличие от истинного значения, уровень значимости составляет 5% Чай. Точно так же IQ немного отличается от нуля. Если используется правильная спецификация, результат Татом выглядит так: d> = -11782 + 21635 (6,20) (1851) (137) Здесь постоянная оценка лучше, но коэффициент оценки изменения S недостаточно (эффект удачи оказался относительно большим Не важно).
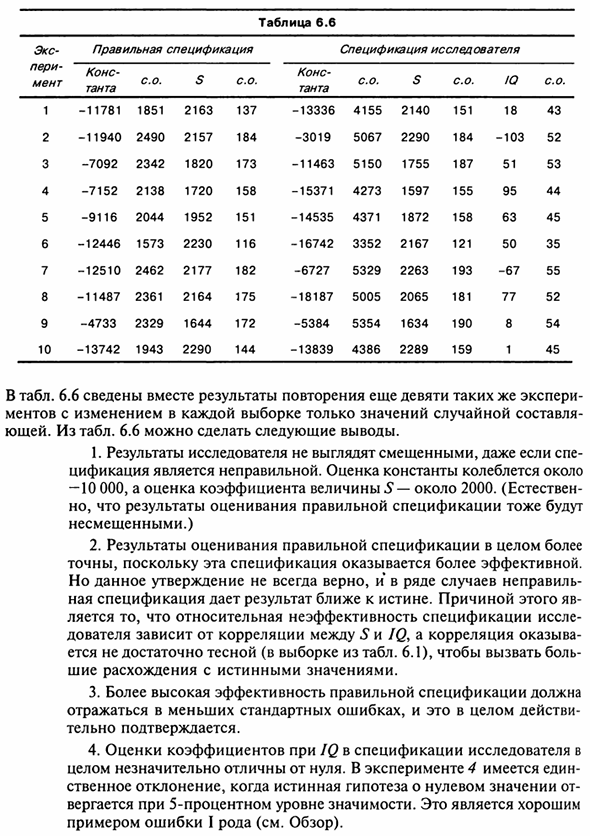
Опять же, вы не можете полагаться на результаты одного эксперимента. В таблице. 6.6 суммирует результаты повторения одного и того же эксперимента еще девять раз. Полицейский, который изменяет только значение случайного компонента в каждой выборке Другими словами. Со стола. 6.6. Можно сделать следующие выводы: 1.
Даже если результаты исследований предвзяты Цитата неверна. Определенный оценочный диапазон —10 000, а расчетный коэффициент для S — около 2000. Тем не менее, результаты оценки правильных спецификаций Объективный. ) 2. В результате оценки правильных спецификаций в целом, Эта спецификация точна, потому что она более эффективна.
Но это утверждение не обязательно верно, а иногда и неправильно Эта спецификация дает более верный результат. Причина в Относительная неэффективность спецификаций рассматривается. Коллайдеры зависят от корреляции между S и IQ. (В образце в таблице 6.1) недостаточно близко, чтобы вызвать боль Противоречие с истинной ценностью. 3.
Более высокая эффективность с правильными характеристиками Отражено в меньшей стандартной ошибке, которая обычно Полностью подтверждено. 4. Оценка коэффициента IQ в спецификациях исследователя Обычно немного ненулевой. Есть один в Эксперименте 4 Истинная гипотеза нулевого значения из Он упал на уровне значимости 5%.
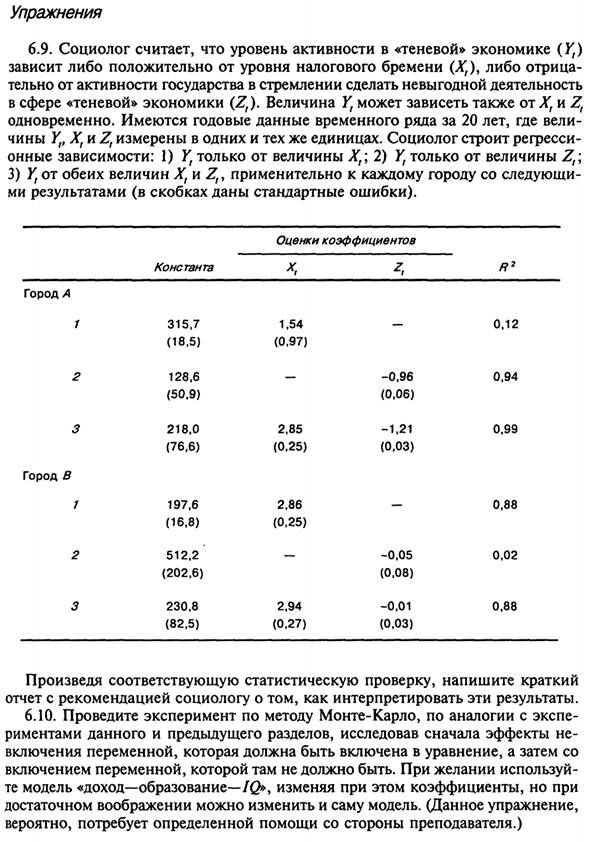
Как приятно Пример ошибки первого типа (см. Обзор). 180 упражнения 6,9. Социологи верят в уровень активности в «теневой» экономике (Y {) Положительно зависит от или отклонить уровень налогового бремени (Xt) Усилия, направленные на то, чтобы сделать деятельность прибыльной, зависят от действий государства В теневой экономике (Zr). Значение Yt также зависит от Xt и Z.
В то же время Есть 20-летний годовой ряд временных данных. Значения Yt, Xt и Zt измеряются в тех же единицах. Социологи строят регресс Зависимости: 1) Yt — только значение Xt 2) Yt — только значение Z; 3) Yt от количества Xt и Z, применяется к каждому городу следующим образом Мой результат (стандартная ошибка показана в скобках).
постоянная Оценка соотношения Город А Город Б 315,7 (18,5) 128,6 (50,9) 218,0 (76,6) 197,6 (16.8) 512,2 (202.6) 230,8 (82,5) 1,54 (0,97) — 2,85 (0,25) 2,86 (0,25) — 2,94 (0,27) — -0,96 (0,06) -1,21 (0,03) -0,05 (0,08) -0,01 (0,03) 0,1 2 0,94 0,99 0,88 0.02 0,88 Напишите короткое предложение после соответствующей статистической проверки Отчет, который рекомендует социологам, как интерпретировать эти результаты. 6,10.
Выполните эксперимент Монте-Карло, похожий на эксперимент В этом разделе и в предыдущем разделе мы рассмотрим первое влияние Включите переменные, которые должны быть включены в уравнение Содержит переменные, которых там быть не должно. Используйте по мере необходимости Это модели «доход-образование-IQ», которые изменяют коэффициенты, Если у вас достаточно фантазии, вы можете изменить саму модель. (В этом упражнении Может понадобиться помощь учителя. )
Смотрите также:
| Моделирование | Замещающие переменные |
| Влияние отсутствия в уравнении переменной, которая должна быть включена | Проверка линейного ограничения |
Если вам потребуется заказать решение эконометрики вы всегда можете написать мне в whatsapp.

