Оглавление:





Влияние температуры и объема на термодинамические функции конденсированных фаз.
- Влияние температуры и объема на термодинамические свойства конденсированной фазы Рассчитайте термодинамическую функцию, используя температуру и объем в качестве независимых переменных.
Поскольку давление, необходимое для выраженного (например, 10%) изменения объема конденсированной фазы, настолько велико, что приближенное уравнение состояния не может быть применено и должно использоваться полное уравнение (12.18). Интеграция в 2 этапа.
Формула для внутренней энергии может быть получена путем объединения формул (2.8) и (4.41). (12.32). Людмила Фирмаль
И первое, что мы собираемся сделать [Т = 0; в = г (0, 0)] К| т, я;(0,0)]. [Т, я? От (0, 0)]до[T, v], где v (0, 0) — молярный объем при абсолютном нуле температуры и нулевом давлении. Ладно! = У(0,0) + ЛКВ (Т, 0) ДТ + Дж дифференциальный клапан. (12.33) И затем И затем Где n — (0,0) — внутренняя энергия при T = 0 и i. = i; (0,0), а cv(T,0) — постоянная объемная теплоемкость, равная i>(0,0).
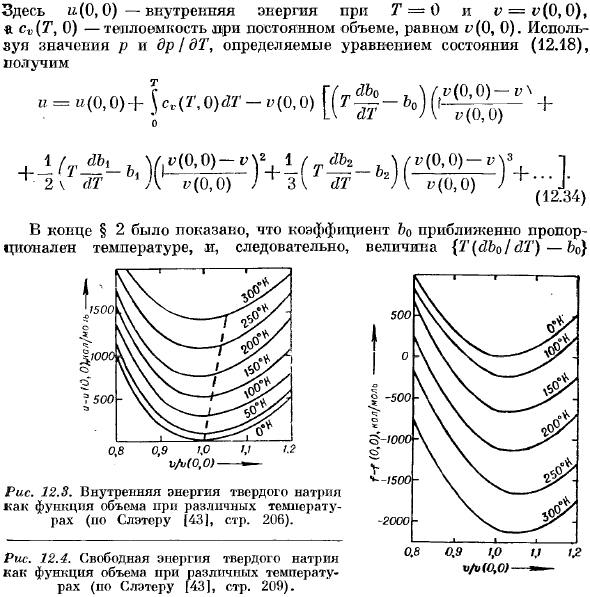
Используя значения p и dr / dT, определенные уравнением состояния (12.18), получаем следующее: «=»(0,0)+ | с <Г.0) Л—, (0,0) [(г§ -+ >> / У(Г, 0) Рисунок 12.Свободная энергия твердого натрия как функция объема при различных температурах(Слейтер [43], p. By 209). Рис. 12.3
- Внутренняя энергия твердой равнины как функция объема при различных температурах (Слейтер(43), p. By 206). _ (М0. 0) — vV 1(t * b_ \ M0. 0) — vy 1 В конце § 2 была указана величина{t (dboldT) −60}, так как коэффициент bo почти пропорционален температуре. Очень small. At при этом коэффициент b \практически не зависит от температуры, поэтому величина{T {dbijdT) — fci}примерно равна-bt. Таким образом, вы можете почти написать т. И=«(0,0)+ 5 эВ (T, 0) dT +±MO,0) pMjp) 2. Поэтому внутренняя энергия должна иметь минимальное значение т. «(0,0)+ \ СV (Т, Г) ДТ о v = i; увеличивает параболический для vt по сравнению с (0, 0) и^(0,0).
То есть, применяется как положительное, так и отрицательное давление. Вышеизложенное показано на рисунке. 12.3, внутренняя энергия твердого натрия изображена как функция объема при различных температурах. Пунктирные линии соединяют точки, где давление равно нулю. То есть, (7*, 0). Формула энтропии выводится из формул (4.2) и(4.38). ( „).- что?= QAZh <■■> Но, как вы уже видели (ср.(12.2) и (12.4))、 (Я) -; — (£),■ В результате производная (ds / dv) m равна отношению коэффициента теплового расширения и коэффициента сжатия.
Это легко измерить. (См. таблицу 12.1) T — > 0, a -?Так как −0, а% стремятся выйти на определенный предел, энтропия при низких температурах не зависит от объема, что соответствует теореме Нернста. Получить интеграцию(12.35) ( § ) (12.37) С т hsch “ Д2 Дж» 2-й интеграл — это формула i(12.л8)может быть оценена так же, как и предыдущий метод. Наконец, свободная энергия Гельмгольца на моль определяется следующим соотношением: ф = п-ц. (12.38)) Объедините (12.33) и (12.37) и перейдите к интегралу 7 от double} (см. (4.20))) Значение/- / (0,0) натрия показано на рисунке. 12.4. Заметим, что согласно (4.29) производная от/относительно T и v равна * * * * * * * * * * * — (21 — <«>
Так что минимальное значение кривой f-v соответствует нулевому давлению. Соответствующим значением объема v является нулевое давление и равновесный объем при различных температурах. Минимальное положение из-за повышения температуры за счет теплового расширения смещается на большую величину и.
Наконец, следует отметить, что физический смысл обусловлен только той частью кривой, которая расположена слева от минимума и соответствует положительному давлению. Людмила Фирмаль
Смотрите также:

