Оглавление:




Влияние способов закрепления концов стержня на величину критической силы ркр
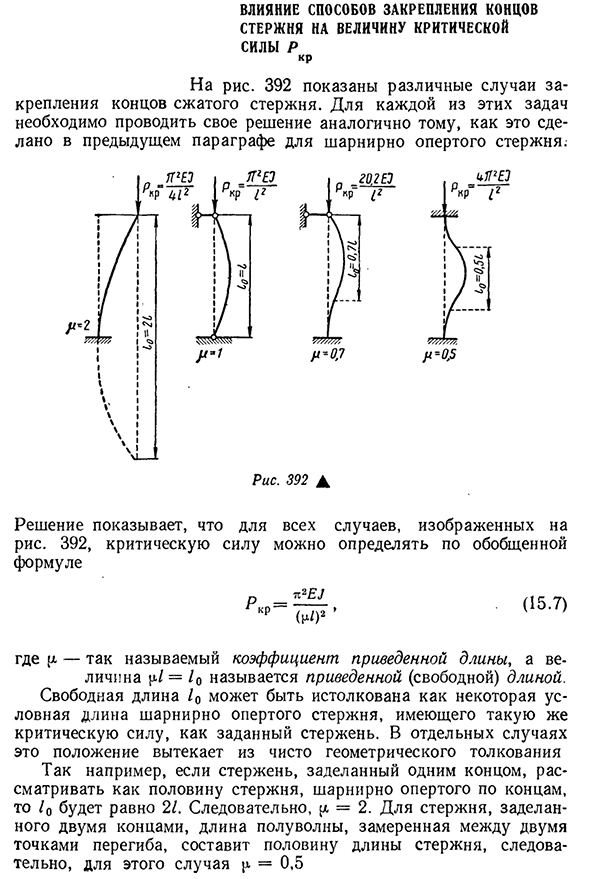
- Влияние способа затягивания концов Придерживайтесь жизненно важных ценностей Мощность Р кр. Для риса. 392 указаны различные случаи фиксации концов сжатого стержня. Для каждой из этих задач
необходимо осуществить ее решение таким же образом, как это было сделано в предыдущем пункте шарнирной опорной штанги. Это решение показывает, что для рисунка. 392, критическая сила
Все случаи являются、 ^ЦР (Я-/)2′(15.7) Где[l — так называемый Людмила Фирмаль
коэффициент редукционной длины, а значение|l / = / 0 называется редукционной (свободной) длиной. Свободная длина / 0 может быть интерпретирована как некоторая условная длина поворотного опорного стержня, имеющего ту же критическую силу, что и данный стержень. В некоторых случаях это положение следует чисто
геометрической интерпретации:например, стержень, запечатанный на одном конце, считается половиной стержня, шарнирно закрепленного на конце, и / 0 равно 21 и, следовательно, RS=2. Для стержня, запечатанного на двух концах, половина длины волны, измеренная между двумя точками перегиба, равна половине длины стержня, поэтому в этом случае p=0,5. 465P R и m e R. Рассмотрим
- я I-го типа на одном конце (рис. 393). Предположим, что в поперечном сечении находится число двутавровых балок 22, то, согласно ГОСТу (Приложение 1), находим момент инерции и поперечное сечение: ЖЖ.* Рис 393D =2550slg4; $ И =157s, H4; P=30,6 см2. Модуль упругости стали E=b=2,1-10E кг / см2; длина стержня/=4М=400 см; коэффициент свободной длины в этом случае[l=2. Естественно, стержень теряет устойчивость в плоскости с наименьшей жесткостью, поэтому приходится брать наименьший момент инерции. По формуле Эйлера
мы вычисляем=5079 кг. (2•400) 2 Критическое напряжение Пять тысяч семьдесят девять 30.6 =166 кг / см2. Как видно из полученных расчетов, стержень теряет устойчивость при значительно меньшем напряжении, чем предел упругости и меньшем основном допустимом напряжении. Для обеспечения устойчивости стержня необходимо сделать допустимое усилие меньше критического. Поэтому для этого стержня напряжение сжатия должно быть меньше 166 кг / см2. Применяя формулу Эйлера для определения критических сил
сжатого стержня, можно определить степень устойчивости различных форм в Людмила Фирмаль
главной плоскости, которая зависит от способа фиксации стержня. Если стержни неподвижны, так что свободная длина при изгибе в обеих основных инерционных плоскостях одинакова, то при расчете РКР необходимо принять минимальный момент инерции, так, например, для колонны, замкнутой на одном конце и свободно замкнутой на другом конце, поскольку сила, соответствующая изгибу этой плоскости, становится минимальной. 466 когда стержни
неподвижны, при изгибе в одной плоскости можно определить две критические силы, если коэффициент свободной длины отличается от коэффициента свободной длины Р-2р Ри изгиба в другой плоскости.: (15.8) Вот И Ты! Y2-главный момент инерции к главной оси. Из двух существенных сил, найденных по формуле (15.8), для расчета берется наименьшее значение. Это ставит вопрос о разумном типе поперечного сечения для сжатого стержня. В случае P1=P2, т. е. если способ фиксации стержня обеспечивает потерю устойчивости
одинаковой формы в двух основных инерционных плоскостях, то два рациональных сечения, например, если сечение состоит из двух каналов(фиг. 394), расстояние между этими центрами тяжести должно быть определено из условий Около, Около Рис 394А Если момент инерции одного канала равен Ug,а поперечное сечение P определяет расстояние a, то можно записать: ох \ 2 Два. / 2-2] 4-РГ Во всех остальных случаях рационального сечения две важные силы
будут равны: Р = Р . 1 1cr l2cr* Уравнение (15.8) для этих двух критических сил, дает следующие условия равноудаленности : 2/2 • N1N-2 467 однако дело в том, что при определении размеров сжатого стержня учитываются многие конструктивные соображения, поэтому необходимо учитывать равноудаленные условия двух направлений стержня. В некоторых (редких) случаях существует такой способ фиксации обоих концов стержня, при котором устойчивость достигается одновременным изгибом оси стержня в двух плоскостях, например, если конец стержня представляет собой цилиндрический шарнир, а оси вращаются друг с другом на угол, не равный 90°, то потеря устойчивости на этой оси обычно решается в специальном курсе устойчивости конструкции.
Смотрите также:

