Оглавление:


Влияние концентрации напряжений
- Влияние концентрации стресса В непосредственной близости от места, где применяется концентрация, рядом с канавкой, концом отверстия, местом, где форма тела внезапно изменяется, и явление,
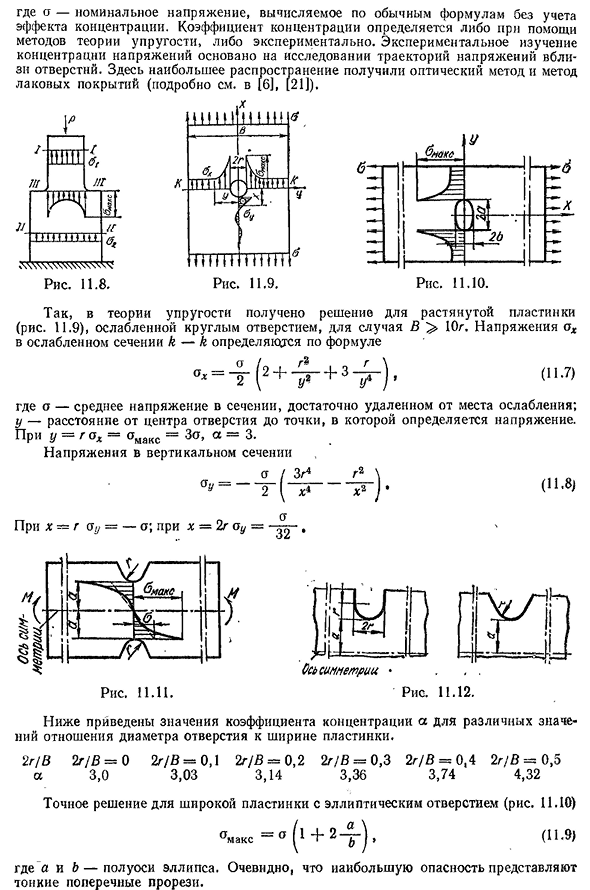
при котором местные напряжения, такие как выемки и трещины, резко возрастают, называется центром. н и у. Например, если стержень, показанный на рис. 1, сжат 11,8, напряжение s-P R
Разделы 1-1 и II II можно определить по обычным формулам ~ -p ~> ~~ p ~. В Людмила Фирмаль
секциях III-III напряжение распределяется неравномерно, увеличиваясь к концу стержня и уменьшаясь к середине. Максимальное напряжение в этом разделе выражается как: ° Макс-около 1 ‘ Значение а называется коэффициентом концентрации.
Общий случай STm x (11.6) Где st — номинальное напряжение, рассчитанное по обычной формуле без учета влияния концентрации. Коэффициент концентрации определяется с помощью методов теории упругости или экспериментальным путем. Экспериментальное исследование концентрации напряжений
- основано на изучении траекторий напряжений вблизи отверстия. Здесь наиболее широко используются оптические и лаковые методы нанесения покрытий (подробности см. В [6], [21]). Следовательно, в теории упругости, если случай 13> южнее, получается решение пластины расширения, ослабленной круглым отверстием (рис. 11.9). Напряжение в ослабленной части k-k определяется как (А.7) Где o —
среднее напряжение сечения вдали от места затухания. y — расстояние от центра отверстия до точки, в которой определяется напряжение. Когда y = r, oh = omax = 3o, a = 3 Напряжение вертикального сечения ст / зг4 Ст. При x = r = -o; x = 2r, oh =, Рисунок 11.11. Ось симметрии тфл «и ——— IL Рисунок 12.12. Ниже приведены значения коэффициента концентрации a для различных значений отношения диаметра отверстия к ширине пластины. 2 г / В 2 г / 13 = O 2 г / В = 0,1 2 г / 13 = 0,2 2 г / В = 0,3 2 г / В = 0,4 2 г / В = 0,5 a 3,0 3,03 3,14 3,36 3,74 4,32 с
овальной шириной отверстия Точное решение для широкой пластины (рис. Людмила Фирмаль
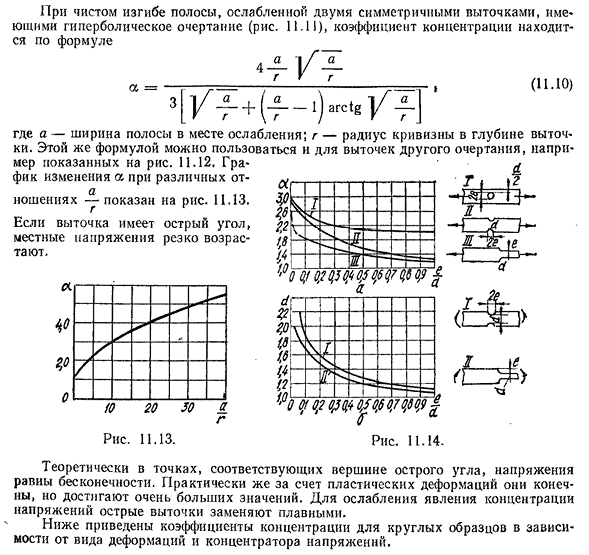
11.10) ° max 0 ^ 1 4-2 j, (11.9) где a и b — полуоси эллипса. Очевидно, что наибольшую опасность представляет узкая поперечная канавка. Чистая кривая полосы ослаблена двумя симметричными углублениями 237 гиперболической формы (рис. 11.11), коэффициент концентрации определяется выражением (11.10) Где а ширина полосы, где она ослабевает. g — радиус кривизны глубины поднутрения. Одно и то же уравнение можно использовать для
углублений с различными формами, такими как показано на рисунке 3. 12,12. График изменения a для различных отношений показан на рисунке. 11,13. Если в подрезке острый угол, местное напряжение быстро увеличивается. 4 * р р но 0 $ 0,2 0 ^ 0,50,6 0,70,60,9 $ 0 Рисунок 11.14. Теоретически напряжение бесконечно в точке, соответствующей острой вершине. На практике они конечны, но достигают очень больших значений из-за пластической деформации. Чтобы облегчить явление концентрации напряжений, острый подрез заменяется гладким. Ниже приведен коэффициент концентрации круглого образца в зависимости от типа деформации и концентрации напряжения части.
Смотрите также:
| Вид деформации | Влияние абсолютных размеров детали |
| Влияние асимметрии цикла. Диаграммы предельных напряжений | Влияние чистоты обработки поверхности и внешней среды на предел выносливости металлов |

