Оглавление:












Влияние гироскопических сил на вынужденные колебания твердого тела. Самоцентрирование
- При составлении дифференциальных уравнений для малых движений твердых тел можно применить теорему о движении центра инерции системы материальных точек и применить теорему об изменении главного импульса системы материальных точек относительного движения к точке инерции. Эти теоремы используются в виде подраздела b данного раздела. Формула 1 2 3. Дифференциальное уравнение вынужденной вибрации рассматривается в разделе 1 этого раздела, а уравнение свободной вибрации зависит от наличия силы заклинивания и ее правильного момента. Технически очень общая категория возмущающих сил включает силы, вызванные статическими и динамическими дисбалансами в Роторе.
Статический дисбаланс обусловлен смещением центра инерции ротора от геометрической оси вращения. Активный Дисбаланс является результатом наклона главной оси инерции твердого тела относительно геометрической оси вращения. При решении задачи определения вынужденной вибрации твердого тела с 4 степенями свободы рекомендуется следующая последовательность действий 1 Выберите обобщенные координаты. 2 с помощью теоремы о движении центра инерции построить 2 дифференциальных уравнения для движения центра инерции твердых тел.
При определении силы реакции балки эпициклический механизм, материальной точкой, сосредоточенной в середине балки ого приближение законно, если размеры механизма малы по сравнению с длиной балки). Людмила Фирмаль
Выражение главного момента импульса системы в движении относительно центра инерции и выражение главного момента центра инерции твердого тела и внешней силы на оси поступательного движения. 4 Напишите еще 2 дифференциальных уравнения малых колебаний, используя теорему об изменении основного момента импульса в движении относительно центра инерции. б найти конкретное решение неоднородной системы дифференциальных уравнений, определяющее вынужденные колебания. Задача 18.43 горизонтальная жесткость массы M ротор вращается с постоянной угловой скоростью 2 упругие опоры A Модуль жесткости опоры слева c1 справа ca. Расстояние между опорами I.
Расстояние от центра тяжести Ротора C до опоры равно опоре Bt и далее равно. А — момент инерции ротора относительно оси симметрии, Б-момент инерции ротора относительно оси, проходящей через его центр, перпендикулярный оси вращения. Если центр тяжести Ротора находится Е в стороне от геометрической оси, а главная инерционная ось ротора вблизи геометрической оси образует последний угол 6, то это определяет вынужденную вибрацию Ротора, вызванную его статическим и динамическим дисбалансом. Ось и центр тяжести образуют двугранный угол, равный е, через геометрическую ось и главную ось инерции.
Также находят закон вынужденного движения ротора и определяют предельное значение координат центра тяжести ротора при неограниченном увеличении угловой скорости ротора и угла отклонения главной оси инерции от геометрической оси ротора. А. С. керзой, самоцентрирование и балансировка жесткого Ротора, вращающегося с двумя упругими опорами, доклады АН СССР, том 110 Решение. Исходит из дифференциального уравнения движения ротора, полученного в предыдущей задаче. Л1Рс — bu1-с г КБМ — Ви-cizi Дурь-по — zacaZa-ZxCiZj Dsou ВР ytcilt yic1li.
Если представить координаты точек геометрических осей Ротора на пересечении этой оси с центром тяжести Ротора перпендикулярно оси вращения и на пересечении с плоскостью через центр тяжести Ротора, y, z, то координаты центра тяжести будут следующими с. Г coserf, 1 zс з esinerf. J 1 Р представляет собой угол между проекцией главной центральной оси на плоскость XY и осью X. Угол между проекцией геометрической оси на плоскость XY и осью X, обозначается па. Эти углы являются П па 6 Кос Фэр-Е, 3 Где erf-e — угол между плоскостью, в которой присутствует угол 6, и плоскостью xy.
Аналогично, угол между проекцией главной оси инерции на плоскость XZ и осью X указывает на y, чтобы найти угол между проекцией геометрической оси на плоскость XZ и осью X. Т Йа 6sin ФЗО-с. 4 Присвоение найденных значений yy, Zq, P и y дифференциальным уравнениям движения ротора 1 AfJ OlVi Л1 е cos at МС cxZi с, Z, Л4eshsin эрф, я- 5 Дор — быт ctltzt — б-д о 8 грех Фэр-е Дшу, Джит б-ка, Дж а-СХ Йи Б-Д Е 8 вида COS в-е.
Правая часть этих уравнений-возмущенный фактор, вызванный статическими и динамическими дисбалансами Ротора. Используя отношение fe A l-i l , установленное в предыдущем выпуске g- Одновременных уравнений б И 4JU-1 cx yj c, Zy8 Mela cos at, M Zi А За, Ди-Тей Cjtei Мела грех и, Лю СР-А — Б ст −20 raZaZz, — B — sin — e , Лш,- A в J,-A CT LYIT-CT lyi в-ct W 6 COS w — e. Полученная система линейных неоднородных дифференциальных уравнений с постоянными коэффициентами представляет собой колебания малого Ротора, вызванные статическими и динамическими дисбалансами.
Решение для этой системы состоит из общего решения для системы без правой стороны и конкретного решения для полной системы. Общее решение системы без правой стороны найдено в предыдущей задаче—оно соответствует свободной вибрации Ротора. конкретное решение системы, которое выглядит для YT я, данные БЖ греха, Зи-в Sin в В2 в COS со, то YT а COS при В8 греха, р в Sin в В4, определяет необходимые вынужденных колебаний.
Чтобы найти значение постоянной, b , назначьте решение 7 уравнению движения 8.Поскольку эти уравнения должны быть заполнены в любой момент времени, сумма всех членов, включая коэффициент cosw , и сумма всех членов, включая коэффициент sin at, должны быть индивидуально уравнены до zero. As в результате вы получите 2 системы алгебраических уравнений. Ma IgOi-Z1fl8 caZa8 Mela1 Ма Заа, — , 0, г я, са я, — Мела — Liu2 0, ч Ба я,-значения i0 ctltlat с Я, , Д что б-л 6й потому что е 17 Аа я, — аа -Ба И8-И1 — ЦС в И8-с Я, б-а 16а потому что е И затем Ма проекта — а С Би caZb8 0, Zjb2- Л crlbg ctlbt О Лю б-А Ба БТ-а caZaZba Cgljbt- Б-Л 6Zo синус, 10 Лю а-БЖ Ба Б-а cmbbбыл cMbg — Б-а 6la грех е.
Из этих 2 систем можно найти значения всех 8 констант a , A b B B b3, b4, так что конкретное решение удовлетворяет исходной системе дифференциальных уравнений. Самый простой способ определить эти константы-сложить и вычесть первые 2 уравнения каждой системы и последние 2 уравнения и получить их из первой системы. Цил о — Здж — AfZi о -ПНО о8-а 0, 11 Б А Е — М ЗДЖ а — Флорида — В А cA o8-a 0, 12 A4Z8w CjZ aj o, — Mlia — ctt a, aj 13 Ф Б-А О -данные, нлл — Б-а о см ПДР а 2 B-A Z6cocos e.
Аналогично, из 2-й системы Af cxZ bx-b8 — Af ZlW — c8Z b8-b4 0, 15 Б-а -CjZZ, ъ-б — б-а о ХС б -БТ 2 B-A Z6w sine, 16 AlZjW C1Z bi b. — AfZjO — c, Z b, b, 0, 17 Б А 0 — КЭЗ Дж ьх Б — Б а о м В8 б 0. 18 подумайте вместе уравнение 11 12 17 18 представляет собой по существу группу из 2 однородных уравнений относительно суммы и разности полученных величин. Если Л О я Л Е CjZZaJ A4Z8o ЧТЗ — — B A w — dZZJ M1W — c, Z 0, 19 Эти же уравнения Тривиальные решения 01 0 а, 04 ба — б В8 — ВХ.
- Остальные формулы 13 14 15 16, если вы назначаете найденное значение нужной константы в поле: AlZaffl с з ОА- A4Za 0 -С З А8 Mela1 Б г О2-ClZZa ОА — Б-а о с Z8Z о, Б-а 6Z диджей удобно AlZ caZJbi- AlZ1w — c2Z bs O, 1 Б-А Ж — ка я к — Б-А Ж С З, З В8 Б-а апельсин SZw е. Теперь вы легко найдете все необходимые количества. В дальнейшем О Б-а о С. Z8Z М1 ХЛЛ — B-D — q ZJ M 1y — c2Z 0, 22 Константы будут равны PC l4e- 1- — AfZjO — c2Z B-D b 1 2cose , 23 Ий 1LMSh —а — С14Л- — Л1 2Ш СХ б-я 6о 2 потому что е, 24 Б2 — A1Zi я 2-с, Z Б-а 1ба грех Е 25 Ba — 1414 1 u1 B-D Zfiio sin c.
Вместо константы b2 a2, at, blt bt, b bt, новая константа g2, g. Вводя соотношение ej-cj-ricosx, b2 −5 r1sin 2 ОГА А4 r2cosi , В8 -В4 Р грех и J Перепишите выражение 8 в следующем формате А Р2, потому что в-Х, 1 и Z2 R2 и грех МЗ-х, я У2 р, потому что ВЗ-Ф, я и Z2 r2sln з-ф. 28 На основании формулы 28 делается вывод, что вынужденные колебания Ротора, вызванные статическими и динамическими дисбалансами, представляют собой прямую прецессию с угловой скоростью w, равной угловой скорости Ротора. Заметим, что статический и динамический дисбаланс этой системы не может вызвать вынужденных колебаний, которые соответствуют обратной прецессии ротатора.
Решить предыдущую задачу в предположении, что эпициклический механизм установлен па упругой балке, которая прогибается па 1 см под действием силы, равной с кг. Людмила Фирмаль
Теперь находим предельное значение константы, которое определяется уравнением 23 — 26, и увеличиваем угол до неограниченной степени Скорость НТ Z26 потому что э-э, Лим А3 ti6cose-е. Лим Би Z16sine Лим В8 Z26 грех. Вводя постоянное предельное значение в выражение 8, находим координатное выражение для o oo. Лим Цзи — COS при lt6 потому что в-е, Лим на ZX — е син на 46 греха В-Е, 1 им ут — е COS при S8, и потому в-е, Лим ЗТ — е син на Z26 грех В-Е. 30 Для определения предельного значения координат центра тяжести ротора и отклонения главной оси инерции от геометрической оси ротора используется формула 2 3 4 подставляется предел координат 80.Используйте зависимости 6.
В результате Лим Us 0 Лим 0 Лим с 0 Лим г 0. 31 В результате при неконтролируемом увеличении скорости вращения несбалансированный статический и динамический Ротор стремится совместить ось вращения с главной центральной осью инерции. С неограниченным увеличением угловой скорости, твердый Ротор вращая с 2 эластичными поддержками помещен, исключающ статические и динамические разницы. Ротор с 4 степенями свободы вращение вокруг оси не учитывается обладает замечательным свойством самоцентрирования. Это свойство широко используется при проектировании современных высокоскоростных машин.
Задача 18.44. В условиях предыдущей задачи определите критическую угловую скорость вращения ротора если отсутствует сила трения. Важным является значение угловой скорости вращения ротора, при котором амплитуда вынужденных колебаний возрастает бесконечно. Solution. As как видно из предыдущей формулы задачи 8, координаты точек Ротора бесконечно возрастают с коэффициентом alt bt. От равенства 23 до 26, это Л со Б-а САС мл cx1 — Б-Д О2-С1 71 A44yu-с, ф 0. 1 Представляет функцию a e в виде a e V-E aH cj c, — E 4-JL Ci J saf-c P 2 и исследовать. Следовательно, значение w равно 0 найти значение f, w. в этом случае нужно различать 2 случая B A и A B. Результаты расчетов сведены в таблицу. в Ф.
Из таблицы видно, что в случае B A Формула 1 имеет 2 положительных вещественных корня 0j и coa. То есть, резонанс возникает при этих 2 значениях угловой скорости rotor. In в этом случае критическая угловая скорость имеет 2 значения Для 2-го случая, для A B, выражение 1 имеет 1 положительный вещественный корень i. то есть ротор имеет 1 критическую угловую скорость, w1 1 Упомянутый в 2 эластичных нюансах 1 Критическая угловая скорость жесткого подшипника Ротора определяется как корень квадратного уравнения. … л я б-а G 2M BX Куда 3 Ки Ка — с ctZJ. При Л 0 уравнение 3 дает критическое значение угловой скорости без учета эффекта гироскопа.
До сих пор при определении вынужденной вибрации Ротора мы принимали fi ф0. А 4 Найдите разницу А — 2 q2 q q-Ma. 5 Из 5, в условии 4, Если ei etjb-Meo2 и оф0, функция A E не исчезнет. Величина ab bt, найденная в предыдущей задаче и условии 4, является начальным дифференциальным уравнением движения.
Поэтому в данном случае Те же резонансные колебания и критические угловые скорости, которые уже были определены в уравнении 3.На этом основании можно сделать вывод, что функция не возникает, когда Ротор подвергается воздействию возмущающих сил, вызванных статическим и динамическим дисбалансом резонансных колебаний, соответствующих исчезновению. Однако под действием других возмущающих сил, изменяющихся с частотой, равной угловой скорости ротора, может возникнуть резонансная вибрация, соответствующая исчезновению.
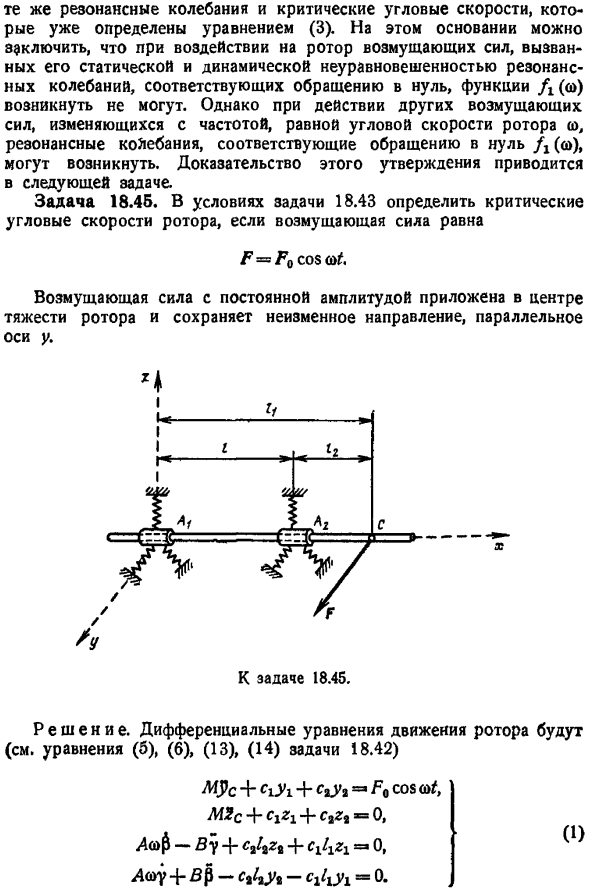
Доказательства этого утверждения приводятся в следующем вопросе Задание 18.45.В условиях задачи 18.43 критическая угловая скорость ротора определяется, если возмущающая сила равна Ф потому что кроватка ФА К центру тяжести Ротора прикладывается возмущающая сила постоянной амплитуды для поддержания постоянного направления, параллельного оси Y. Один Выпуск 18.45. Решение. Дифференциальное уравнение движения ротора уравнение в вопросе 18.42 b 6 13 14 см. также КРД ки я коэф ФТ COS при Си Ви CaZt 0 -г С, , если ЗТ clZ1Zi 0 ЛСОУ — Ки ЛПИ 0. Если мы подставим формулу для усов, zq, , V см. формулу в вопросе 18.42 1 — 4 М ЛЛ — С1 У1 п.
Решение этой системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами является суммой общего решения системы без права и частного решения полной системы. Общее решение для системы без правой стороны уже найдено. Это уравнение свободной вибрации Ротора см. задачу 18.42.
Конкретное решение всей системы, определяющей вынужденную вибрацию Ротора, предлагается в следующем виде Ай 11 COS при, в Sin в, yt o8cos оз, З2 o4sin оз. Дж Подставляя 3 в дифференциальное уравнение движения 2 и уменьшая его с помощью sin at или coszt, получаем алгебраическую систему уравнений для определения констант alt a, a3 соответственно. ПНО Mlta о ЦТЛ-М Л а в F0Z cxZ MZ2 oa o, c2Z-Л1Zjto oi 0 А 0 ОИ-Асо Оз с з-БО1 О2 c2Z2Z Б О2 А4 0,я А oao4-Aaiai — с Л-Ба в- С21 1 Б ОА А8 0. При сложении и вычитании первых 2 уравнений и последних 2 уравнений cxZ м 1аа о О2 c8Z-М 1 о ое А4 фол Б-А — С З ОИ А — Б-а c1313 о О4 о Cil М4ю ot-аа c8z-AF CO2 es — р.1. Б а о — С14 Дж ОИ-вых.
Из этого уравнения Число 4 Ч — 1 1 1 соединение В А o2 C1ad добро пожаловать на наш сайт Gu1 Б-Л У2 A, В1, В Д А Б С, С 1 2Ф ь з ч FJ Д-Л sdd F F cd Л сУ г-2г. и, Б. F KB-A — , FeHtB A — 1 2f3 2Ы Ф Б-а — МГК Ф Д Б А Ф-см 2, и 2 раз о Формула 6 показывает, что когда A m приближается к нулю, alt ag, at, at будет увеличиваться indefinitely. In решая предыдущую задачу, мы обнаружили, что A o и A не имеют общего roots. So, если A — 0, то A 0 принимает ненулевое значение value. So, если A w мало, то первый член выражения 6 можно игнорировать по сравнению со 2-м. Таким образом, вы можете отбросить первую часть в 6 для приблизительного определения константы. И затем.
Таким образом, уравнение движения точек Ротора, совпадающих с опорными центрами дна и верха, приобретает следующий вид Aicos е, Зи — Фли греха г ascosat ЗТ — А3 греха. Дж 8 Из уравнения 8 видно, что характер колебаний, вызванных силой F вблизи резонанса при соответствующей критической угловой скорости, определяемой из уравнения A 0, соответствует синхронной обратной вращательной прецессии. Критическая угловая скорость обратной прецессии найдена из уравнения см. задачу 18.43. А КВ А В4 M12a CxZ — — 5 A и-cxZZx и Hsha-CjZ О Откуда 9 а СХ фдж Б а Л4 cxZJ КЭЗ Кроме того, эти ценности всегда реальны.
Смотрите также:
Предмет теоретическая механика

