Оглавление:












Влияние гироскопических сил на вынужденные колебания твердого тела с четырьмя степенями свободы. Самоцентрирование
- При составлении дифференциальных уравнений для малых движений твердых тел мы можем применить теорему к движению центра инерции материальной точечной системы и применить теорему к крупным изменениям. Момент импульса материальной точечной системы, которая совершает движение относительно центра инерции. Эти теоремы используются в виде пункта 5 в этом разделе уравнения 1 2 3. Дифференциальное уравнение вынужденных колебаний А пункт о в этом разделе уравнения свободной вибрации обусловлен наличием возмущенной силы и ее правильным моментом. Категория заклинивающих сил, которые очень распространены в технике. Сила, создаваемая статическим и динамическим дисбалансом Ротора.
Статический дисбаланс обусловлен смещением центра инерции ротора вокруг r геометрической оси вращения. Динамика тяжелая неуравновешенность является результатом наклона основного Ось инерции твердого тела относительно геометрической оси вращения. При решении задачи рекомендуется следующее i действие для определения вынужденной вибрации твердого тела с 4 степенями свободы. 1 Выберите обобщенные координаты. 2 использовать теорему о движении центра инерции для создания 2 дифференциальных уравнений движения центра инерции твердых тел. 3 выражение главного момента импульса системы, находящейся в движении относительно центра инерции, и выражение главного момента внешней силы.
При опускании груза со скоростью трос оборвался, и груз достиг дна через Т секунд после момента обрыва троса. Людмила Фирмаль
Ось перемещается поступательно центром инерции твердого тела. 4 напишите небольшое дифференциальное уравнение 2, используя теорему об изменении главного момента импульса в движении относительно центра инерции. Изменчивость 5 нахождение конкретного решения для неоднородной системы дифференциальных уравнений, определяющих вынужденные колебания. Задача 460. Горизонтальный жесткий ротор с массой m вращается с постоянной угловой скоростью 0 с двумя упругими опорами и bp. Опора движется с равномерным упругим нулем. Шансы Жесткость опоры левая и правая КР. Расстояние между опорами. Расстояние от центра тяжести Ротора С до опоры равно опоре В1 2. In кроме того, a — это момент инерции Ротора.
Ось симметрии, в-момент инерции ротора относительно оси, проходящей через его центр, перпендикулярный оси вращения. Если центр тяжести Ротора находится далеко от 1-й оси оси, то это определяет вынужденную вибрацию Ротора, вызванную статическими и динамическими дисбалансами. Главная ось инерции Ротора, близкая к геометрической оси, образует угол 2 от последней. Геометрическая ось и центр тяжести, а также плоскость через геометрическую ось Ось и инерционная ось глаза образуют двугранный угол, равный е.
Найти также закон вынужденного движения ротора и определить предельное значение центра тяжести ротора и склонение главной оси инерции геометрической оси ротора Неограниченное увеличение угловой скорости вращения ротора. Решение. Исходит из дифференциального уравнения движения ротора, полученного в предыдущей задаче. А уя — с, y — l1gs Я ДшЗ-87 — r2s. 2 4— ДС — С. 53 г — г. 2 координаты точки геометрической оси ротора на пересечении этой оси с плоскостью, перпендикулярной оси вращения и проходящей через центр тяжести Для Ротора координаты центра тяжести следующие показать 3 в плоскостях xy и xy и прошептать yy y — — соя из 2 Сент. 2- э 81n о.
Угол между проекциями главной центральной оси по оси x. Угол между проекциями геометрической оси по оси x обозначается 3. 2. Эти углы соединены Мы здесь, чтобы помочь. 2 Крушение 3 Где w — e — угол между плоскостью, в которой существует угол b, и плоскостью xy. Аналогично, через 7 показан угол между проекцией главной оси инерции на плоскость xx и осью x, а также угол между проекцией геометрической оси на плоскость 7 xx и осью x. Мы это выясним 7 3 8 П С — а. 4 Подставляя найденные значения y, s, 8, 7 в дифференциальное уравнение движения ротора 1, получаем Му — -с y, 4-o2 y2 l4ssh соя ш, МХ-7 — neuyash ш В о5 −87 ГБЦ. 2 4 c1a-2 1 — — a a r1p w e, d- 7 и 4-8p2-clu-2 k — a o o соя s — e.
Правая часть этих уравнений-возмущенный фактор, вызванный статическими и динамическими дисбалансами Ротора. Используйте отношения, установленные в предыдущем выпуске 6 И если мы найдем систему уравнений о М Г -г 1 Б г 4 с уч мм потому что Л1 1 2- У5 4-с 1rx 4 — я ь Рыдать Дю y2-5 −4 ц 1 2 я Уч — Б-а корова 1П о — е Ду. .. , -п — стр. 24 год. 2 — Б-4 о 3 со п — е. Полученная система линейных, неоднородных дифференциальных уравнений с постоянными коэффициентами представляет собой малую вибрацию Ротора, вызванную статическими и динамическими колебаниями Дисбаланс. Решение для этой системы состоит из общего решения для системы без правой стороны и конкретного решения для полной системы.
Общее решение системы без правой стороны найдено в предыдущей задаче—оно соответствует свободной вибрации Ротора. Y1 a1 первое решение для полной системы в формате cos 81. 1. А -г БЗ с cos о ал, потому что а Б2 81n СК Р3 Д4 31n ШБ БК с cos о Определите необходимую принудительную вибрацию. Чтобы найти значение постоянной ai, назначьте решение 7 уравнению движения 8. Потому что эти уравнения должны быть выполнены в любой момент Маркеры должны быть равны сумме всех членов, включая фактор cos w, и сумме всех членов, включая фактор ssh yy, separately.
В результате вы получаете 2 системы алгебры Уравнение ju2 — А-Л Оз ь 1А г Д 4 с 1а 4 с АБ я В −4 0 Д3-С7 б д Д4-Д-2 4 4 — Б-д zu1 потому что е Дю Д4-Д2 -ты П3-П — С с — Б-д vu1, потому что е 9 10 И затем Л 8 2 1 — б з Н 4 3 0 8 —с б, — — р 4 о. Л в б-б — в Б-Л Х-ф 4-4 с-Л А oa 8 1n e Лю 8 4- — -bj a, — ад 4-c2 2 a3 — -Б А Б-а oao2 Н. Из этих 2 систем можно найти все значения 8 констант ax, a2, a3 и, b, b b, 3, так что конкретное решение удовлетворяет исходной системе дифференциальных уравнений. Самый простой способ определить эти константы-сложить и вычесть первые 2 уравнения каждой системы и последние 2 уравнения.
Затем из первой системы П1 Х — с, Ф 1 — — П1 1-с УГ- Р1 01 Я Я 4 — с 1 1–1 4Л О2 4 — Л1 с-Л4 0, 12 Ж 8 4-й, г-4Л2 — Ж 8- 7 а34-а4 2Же ш8, 13 i-a w2-c, , 1 a, 4-a — i-a a 8-k А аа Д4 2 b — a du cos e. 14 аналогично найдем следующую из 2-й системы. Вт 4О 2 4-с, — ж, о8-г П3-ад 0, 15 ТСН-а о — р 1 -ад — r-a w— — c -. — си. −2 Б-А 5. 2 81n е, 16 л 2sh8-это, Ф ЛК 4— л, co8-С4 Б3, 4-Б. 0, 17 От o2-c, , А, 4-Б — Б 4-а Вт 4-З б. — Я-ад 0. 18 Уравнения ii 12 17 18 мы будем рассматривать его вместе.
Это по существу группы из 2 однородных уравнений относительно суммы и разности полученных величин. ,. О ДД а1- -е2М, М1 я-с — — i vl w — s. 11, ui, 0. 1-s. , y o, 19 тогда этническая система однородных алгебраических уравнений имеет только самоочевидное решение ВХ — −1. 1-аз 20 Остальные формулы 13 14 15 16 Если вы назначаете найденное значение нужной константы в поле Л4 в с Д — и — с4 а3 Ме — 1 — УП х а — — ОА с, 4 А3 Б-з 8 О потому что е m x c-6, 6, — 1, oi-c, ll 0 -Л ш-с, , — Л-Л и С. Лл b-a 8 81p г. Теперь вы легко найдете все необходимые количества. В дальнейшем 1 — М1.
- Константы будут равны 01 е л б — — М пр-с 1 Б-а os9 потому что 0 1 л г Ми 1 Г А З — С 1 ноября. — Р1 не-е 7 0 поп Я, 101-с Б-А Ю 81n Е, М-7 я 4ю — р б-а ю а. Вместо константы pr a3, b, b, b введем новую константу r, r y, phi, которая связана соотношением l. 1 t 51n Г Р1 Ф 23 21 23 26 1 3, 27 3 — Перепишите выражение 8 в следующем формате р, со Колорадо — р р ш о —Х потому что —, рН Р 81 с. Ш ш —. 28 На основании уравнения 28 делается вывод, что вынужденные колебания Ротора, вызванные статическими и динамическими дисбалансами, представляют собой прямую прецессию с углами. Скорость o, равная угловой скорости вращения ротора.
Следует отметить, что статический и динамический дисбаланс этой системы не может вызвать вынужденных колебаний, которые соответствуют обратному вращению дочерней прецессии. Здесь мы находим предельное значение константы, которое определяется уравнением 23 — 26, в котором угловая скорость безудержно возрастает. Золото d 4 5soze-e — Объектно-ориентированный АУ АА 28 потому что е-ЕС И co 29 Хм, 4 фунта за 8. О оо Золото 1 43 51 pe. О — оо Вводя постоянное предельное значение выражения 8, w Тю — е сов — −4 8 вида cos ш — э, п — оо В золоте 21 −81 p — −4 8 t o — e Вот именно.
Вместе с тем вычисление наибольшего смещения можно легко осуществить, так как для этого достаточно найти зависимость между х и х и, приравняв затем в крайнем положении груза х нулю, определить искомую величину. Людмила Фирмаль
Для определения пределов координат центра тяжести ротора и отклонения главной оси инерции от геометрической оси ротора подставим пределы координат 30 Формула 2 3 4 преобразовать в. Используйте зависимость 6. В результате вы получите hm us 0, и — с Золото Р 0 О — оо Золото 2С 0, п — оо Пятница 0. Вт — ОО 31 В результате, поскольку угловая скорость вращения увеличивается бесконтрольно, несбалансированный статический и динамический Ротор стремится совместить ось вращения с главной центральной осью. Инерция.
С неограниченным увеличением угловой скорости, твердый Ротор вращая с 2 эластичными поддержками могл выполнить и статическое и динамическое Дисбаланс. Ротор с 4 степенями свободы вращение вокруг оси не учитывается обладает замечательным свойством самоцентрирования. Это свойство широко используется в дизайне. Современная высокоскоростная машина. Задача 461. В условиях предыдущей задачи определите критическую угловую скорость вращения ротора если отсутствует сила трения. Важным является значение быстродействующего гайротора с неограниченным увеличением амплитуды вынужденных колебаний. Solution.
Как видно из уравнения предыдущей задачи 8, координаты точек Ротора бесконечно возрастают с коэффициентами. От равенства 23 до 26, это А 3-А ю — — с. — — -. 4 -c, 1-c t 0. 1 Функция, , в виде Вт Б-а, с, — Иш l1l Р s — s, s, 2 и исследуем его. Следовательно, если значение w равно o Я нашел значение 2 n. В этом случае вам нужно различать случаи b a и d b 2. Результаты расчетов сведены в таблицу. Ш Л Д К В Ноль— sl-slg s. Sl 2 4 ОО Н с Таблица p.
Как видно из 629, в случае а уравнение 1 содержит положительные вещественные корни 0 и o4, то есть резонанс возникает при этих 2 значениях угловой скорости. The rotor. In в этом случае критическая угловая скорость имеет 2 значения Во 2-м случае для a b выражение i имеет 1 положительный вещественный корень p. 1 критический для Ротора. 1 1 4 2 Угловая скорость, и я Критическая угловая скорость жесткого Ротора, описываемая в упругих опорах 2, определяется как корень уравнения 2-го порядка 1. Это хорошая вещь. Уй — я ВЛ У, Ы. 3 в. — 2М В-А Куда И. Ч-я-ч Г-Л М Р, Ф 5, — Б Б-а — м р, ф р, о При 4 0 уравнение 3 дает критическую угловую скорость без учета эффекта гироскопа.
До сих пор при определении вынужденной вибрации Ротора f, w 0. Предполагалось, что он равен 0. Л ж 0. 4 Найдите разницу Л -А 2л О4 Т1 ч-a1co. 5 Из 5, при условии 4 функция a o равна c mi и 0. Нашел n назад Дайте значение a, b1, при условии 4, удовлетворяющее исходному дифференциальному уравнению движения. Поэтому в этом случае возникают те же резонансные колебания и критические углы Скорость уже определена в Формуле 3. Исходя из этого, можно сделать вывод, что Ротор подвергается воздействию возмущающей силы. Идентифицируется по его статике и динамике Дисбаланс, резонансная вибрация, соответствующая исчезновению, функция f не может возникнуть.
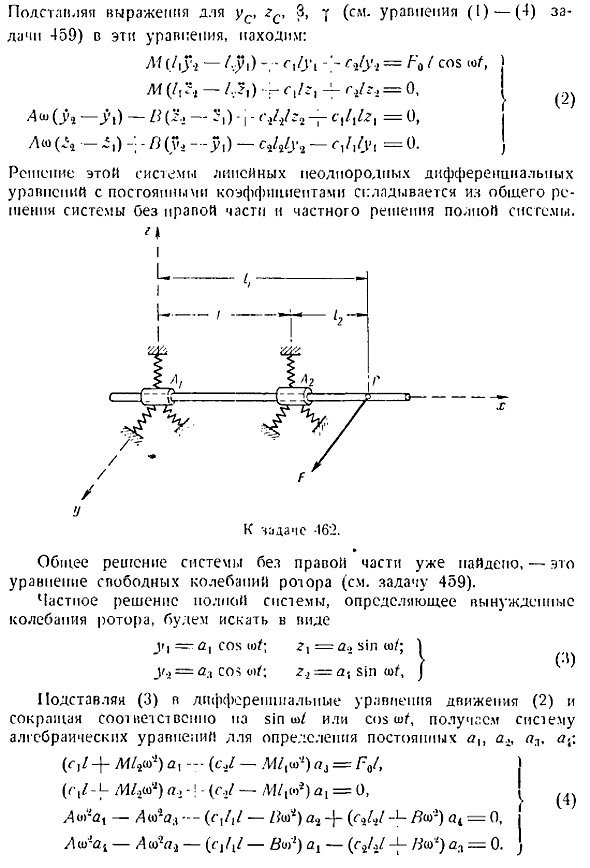
Однако под действием других возмущающих сил, которые изменяются с частотой Резонансная вибрация, соответствующая циркуляции пули, равна угловой скорости вращения ростверка w Происходить. Доказательства этого утверждения приводятся в следующем вопросе Задача 462. При условии задачи 460 критическая угловая скорость ротора определяется, если возмущающая сила равна Р идти, потому что ж. К центру тяжести Ротора прикладывается возмущающая сила постоянной амплитуды, поддерживающая постоянное направление, параллельное axis y. Решение. Дифференциальное уравнение движения ротора выглядит так рассматриваемое уравнение 459 5 6 13 14 см.
Мускат С05 Листья — 7 — — 0, i Если вы не хотите этого делать, вы можете сделать это с помощью следующей команды b — c buy-c 1 y Подставляя формулы усов, 2c, 3, 7 см. Уравнение i — 4 в вопросе 459, получаем следующую формулу Л −4 — 00 1 потому что Л4 М-4 1 т с я. Г — — — — У1 — — 1 С 4 1 Лео. 4- — чч-уу — c4 8 4-y, 0. Разрешимость этой системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами состоит в общем решении системы без правой части полного подрешения.
Общее решение системы белков справа уже найдено-это уравнение свободных колебаний Ротора см. Задачу 459. Конкретное решение всей системы, определяющей вынужденную вибрацию Ротора, предлагается в следующем виде В — А что ж y2 аз с з 3 г Д2 81 л со 2 58581ПО Присвоим 3 дифференциальному уравнению движения 2 и уменьшим каждое pa w или получим алгебраическую систему уравнений для определения констант a a a b al, a. С 1- М 4 О2 — с 1-МК 1 ал перейти г л. 2 О есть. — — с. 2 — М о Д О Ла-ЛЛЛ- С — К РВ рН 0, Л — А1-А-а 2л. 2- С В — О 2 А1 —, С номер 4 ж аз о- Если вы сложите и вычтете первые 2 уравнения и последние 2 уравнения, вы увидите следующее С, Р М 4 А-А ч- гр.
Из этих уравнений вы получаете 6 Формула 6 показывает, что когда f o близко к пуле, a a, b1 увеличиваются неограниченно. При решении предыдущей задачи мы обнаружили, что и 2 o не имеют ничего общего Корни. И так оно и есть. — если 0, то 2 w принимает другое значение, чем bullet. So, первый член выражения 6 настолько мал, что его можно игнорировать по сравнению со 2-м членом, если он мал w. Таким образом, вы можете отбросить первую часть в 6 для приблизительного определения константы. И затем.
Смотрите также:
Предмет теоретическая механика

