Оглавление:








Влияние гироскопических сил на свободные колебания твердого тела с четырьмя степенями свободы
- Для составления дифференциального уравнения малых колебаний твердых тел при наличии гироскопической силы необходимо применить теорему о движении центра инерции системы материальных точек относительно центра масс, а также теорему об изменении импульса системы импульсов. Согласно первой теореме, это Компании ihs МТУ 1 Где m-масса твердого тела. L s, mustache, rf-координаты центра инерции силы тяжести твердого тела в системе координат с фиксированной осью. Проекция главного вектора внешних сил, приложенных к твердому телу. Вторая теорема приводит r к соотношению. Где lsch, лгу, и ds-основные моменты инерции для оси, которая движется поступательно вместе с центром инерции, Н.
Тяжесть твердых тел ut i — главный момент внешней силы a— Относительно той же оси. Когда осесимметричное твердое тело вращается вокруг оси симметрии с большой угловой скоростью 0 и совпадает с малым колебанием объекта оси x, то главный момент импульса твердого тела относительно оси координат, движущейся параллельно центру, до величины 1 равен sj. O 3 −5 т р 3 Где А-момент инерции твердого тела относительно оси симметрии. B-момент инерции твердого тела, перпендикулярный оси симметрии и на любой оси, проходящей через центр инерции тела. P-малый угол поворота оси симметрии, измеренный от оси x плоскости xy. 7-малый угол поворота оси symmetry. It измеряется от оси x плоскости x2.
Просмотрев внимательно решение этой задачи, можно обнару-жить, что равномерное прямолинейное движение груза является следствием соответствующих начальных условий движения (наличие в уравнении (2) постоянного слагаемого Нетрудно подобрать начальные условия движения, при которых груз совершал бы только колебательное движение. Людмила Фирмаль
При исследовании поперечных колебаний малые продольные перемещения твердых тел обычно игнорируются. То есть предположим, что координаты xc не изменяются. Тогда первое уравнение 1 disappears. In кроме того, учитывая равномерное вращение твердого тела, первое уравнение системы 2 также исчезает. Для решения задачи о свободной вибрации твердых тел, которую можно предположить выше, мы рекомендуем следующую процедуру. 1. Выберите 2 системы координат. Первая система-это стационарная система координат-вторая система, плотно связанная с твердым телом. 2. Примените теорему к движению центра инерции, чтобы создать 2 дифференциальных уравнения для движения центра тяжести. 3.
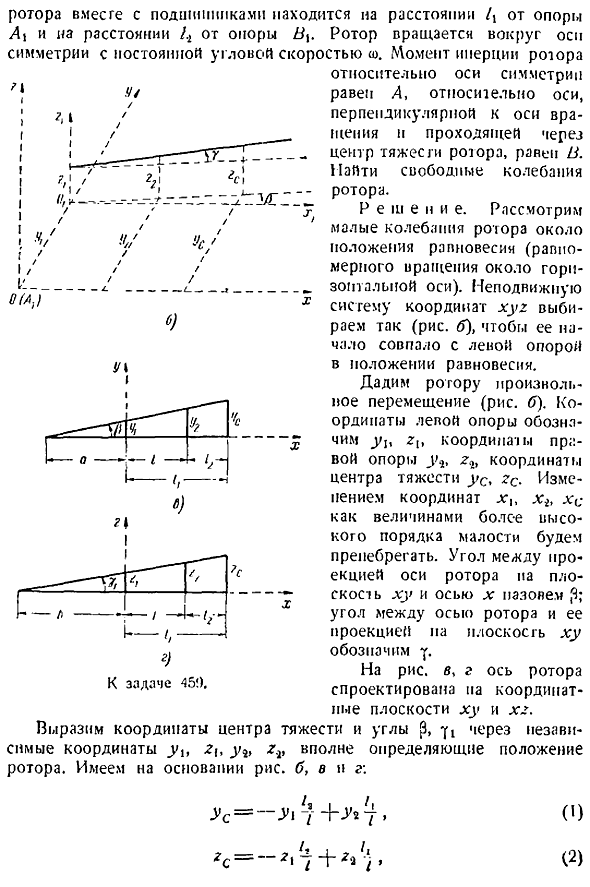
Используя теорему об изменении главного момента импульса при относительном движении относительно оси Наряду с центром инерции, небольшая вибрация твердого тела составляет нижнюю часть остального дифференциального уравнения. 4. Когда вы интегрируете полученную систему дифференциальных уравнений движения твердого тела, вы найдете частоту свободных колебаний, основную вибрацию ротора и общее решение задачи. Задание 459. Твердая масса Ротора поворачивая 2 Упругая опора. 4, и коэффициент жесткости поддержки левой стороны на праве диаграмме а. Расстояние между опорами равно. Центр тяжести Ротора c и подшипник расположены на расстоянии 4 от опоры d. Опора от b до 4 расстояния.
Ротор вращается вокруг естественной симметрии ПО с постоянной угловой скоростью. Момент инерции Ротора д К выпуску 459. Представляет собой координату и угол p центроида, а также координату uy 2b y 2. 1 g Ротор. B, c n d, исходя из рисунка А относительно оси симметрии равно а относительно оси, перпендикулярной оси вращения n, проходящей через центр тяжести ротора, и Б относительно оси вращения ротора. Найдите свободную вибрацию Ротора. Определение рассмотрим малую вибрацию Ротора вблизи положения равновесия равномерное вращение вокруг горизонтальной оси. Фиксированная система координат обруча выбирается таким образом рис.
- Чтобы его начальная точка совпадала с левой опорой положения равновесия. Дайте Ротору любое движение рисунок b. Координаты левой опоры-y Координаты правой опоры — это координаты, обозначенные Центр тяжести усов, 2 секунды. Игнорируйте изменение координаты xn xb xc как меньшее количество заказа. Угол между проекцией оси ротора и оси x в плоскости xy называется 3. Угол между осью ротора и его проекцией в плоскость xy обозначается y. На рисунке vu r оси ротора рассчитаны для координатных плоскостей Ху и Х2.
Основываясь на теореме о движении центра инерции, можно написать 2 дифференциальных уравнения. — s1u1-s9u9, 5 МГС — 6 С правой стороны имеется выступ на соответствующей оси упругой реактивной силы пружины. Приступим к построению дифференциального уравнения малых колебаний ротора вокруг осей, параллельных y и r, проходящих через центр инерции колебательной системы.
Ось х направлена вдоль оси пружины по горизонтали направо, причем начало отсчета находится в правом копие педеформированной пружины. Людмила Фирмаль
До заданного момента импульса в системе Первое основное небольшое количество десятичных знаков-это lx d 0, 7 1-г Дрчр — 8 9 Основные моменты внешней силы относительно нарисованной оси Через центр инерции, рисунок а x msx 7p −0 У. — g1s1 1. 1 1 y02 с использованием теоремы и формулы 8 — 12 об изменении основного момента импульса в движении относительно центра инерции Листья — 7 — 13 ЛАГ 4 g h Формула 5 6 13 14 подставляя значения yc, p, 7 для нахождения y1 y, r, получаем систему из 4 линейных однородных дифференциальных уравнений. — 4П У1- -с У2 0, 15 М, —, , 0, 16 a 1 y2-y1 0, 17 л ш л-А -я Л-Р —г о.
Конкретное решение для этой системы требуется в виде Г о 81p р 4-а y p951n — — х 2, Р3 со Р1 а 22 Р1 а Где ad e, o -, p, a-константы, которые должны быть определены так, чтобы 19 удовлетворяло системе дифференциальных уравнений 15 — 18. Введение 19 в 15 — 18 уменьшает 1n 4 a и sox 4-a, и после сокращения таких членов мы получаем однородную систему из 4 алгебраических уравнений относительно o, О ah. С-1-М1 4- Р4 -мкр о о с, f О2 2 — М1 ок о — l a14-d o o. 2 c1 1 3- — л 3 — — 2 d4 o, 0 bp2-o — bp1 o airol-ashrob 0. Легко показать, что система 20 делится на 2 parts.
Если вы сложите и вычитаете первые 2 уравнения и последние 2 уравнения, вы получите 1 -gg a-g ad-g o2 hell 0 С1 4 л 4 hell 4- м П ад о ВР 4-данные-СРБ о — НОП — ВР 4-данные 4-см О4 4-ад о 3Р air см 1 ад Ашр 4 ад о. Когда вы группируете уравнения, вы получаете o 4 — 3 и систему, чтобы найти ад. C4 — t 4 3 b b v-mcp1 0, 2-4 l 0 ВР 1-Аир-с Т Т 14-В2 — — ВР2 4 — л ИК 4-ЛО Фдж 4 — о 21 И система поиска 01-p3 и o −0. 4-м В1-ад 4- c2r-а, Р3 х, ад о, ВР-Воздушно-е, , о — О2 — — ВР-воздух 4-С О — ад 0. 22 Если уравнять детерминанты системы 21 и 22 до нуля, то получим уравнение-частота. Др н — — — ГС — мр 4- 6 4- v 1 0 23 yar1-воздух-Г, Г, 4-г. 2-Мп — г г, — 1 — 0.
Докажем, что в уравнениях 23 и 24 нет общих корней. Предположим, что существует общий корень. Тогда p p оба уравнения заполняются одновременно. Если вычесть 2-е из первого уравнения, то получим 2 lcop r, 4 — 1-mp 0 То есть общий корень p 0 и 1 1 — m — Однако оба эти значения не соответствуют исходному уравнению. Указывает, что тело частотного уравнения является real. To сделайте это, рассмотрим функцию p rf воздух — 2 — 4-с — ЛГ 2 −4 С 4-С24 25 Л р ДП — воздух-Р, Ф р, 4 — р-4-Мп 4- з, ф, 4-С, в 26 Найти значения некоторых характерных значений аргумента p. П 1 п — оо-оо.
Смотрите также:
Предмет теоретическая механика

