Оглавление:







Влияние гироскопических сил и сил вязкого сопротивления на свободные и вынужденные колебания твердого тела с двумя степенями свободы
- Влияние силы гироскопа на свободную вибрацию. При составлении дифференциальных уравнений для малых колебаний, учитывающих гироскопическую силу, теорема может быть применена к изменению основного момента импульса относительно неподвижных осей координат. Т J — В О. Где Lx, L-L-основные моменты импульса движения относительно неподвижных осей координат x, y, r, F. F — главный момент внешней силы относительно той же оси.
Если осесимметричное твердое тело с неподвижной точкой вращается с большой угловой скоростью вокруг оси симметрии, то это совпадает, когда тело находится в равновесии с неподвижной осью x, А главный момент импульса относительно неподвижных осей координат равен максимуму 1x. ЛК ВБО, И Ly Данные-На, ЛТ Сор — — Б, 2 Где A-момент инерции твердого тела относительно оси симметрии, B-момент инерции к любой неподвижной точке, перпендикулярной оси симметрии, P-малое вращение оси симметрии, отсчитываемое от неподвижной оси x плоскости xy, и P-малое вращение симметрии, измеренное от неподвижной оси x плоскости y-X.
Если при решении задачи динамики движение точки системы разлагается на переносное поступательное вместе с полюсом и относительное по отношению к полюсу, то целесообразно принять за полюс центр инерции системы материальных точек. Людмила Фирмаль
Выберите 2 системы координат неподвижная и движущаяся — начальная точка является неподвижной точкой. 2 Вычислить главные моменты всех внешних сил для неподвижных осей x, y, z и главные моменты импульса для этих осей. 3 найти дифференциальное уравнение малых колебаний системы, используя теорему об изменении главных моментов импульса относительно осей x, y и Z. 4 найти конкретное решение системы и отнести его к дифференциальным уравнениям движения.
Найти частотное уравнение, определяющее собственные частоты системы. 5 кроме того, найти отношение амплитуды колебаний, соответствующих каждой частоте. 6 создать уравнения 1-го и 2-го главных колебаний и общие решения как сумму главных колебаний. Задание 18.35.Ротор с неподвижной точкой 0 вращает ось симметрии Oc и совершает небольшие колебания вокруг неподвижной оси y, r. найти основной момент импульса ротора можно с точностью до 1 секунды. Момент инерции ротора к оси Oc равен А, А К В для главных осей а и в инерции. Решение.
Используйте неподвижную точку O в качестве начала координат и движущуюся систему осей a, b и c, которые являются основными инерционными осями твердого тела в точке O, чтобы выбрать неподвижную систему координат xyz. ЦМР-это пересечение плоскостей AC и xy. Линия узла включается, и углы и y используются для определения положения системы перемещения оси. Составляющая угловой скорости Ротора выглядит следующим образом 0, ориентированная вдоль оси Oc, ориентированная вдоль оси P, ось z y, ориентированная в отрицательном направлении оси Ob. Найти проекцию угловой скорости Ротора на инерционную главную ось a, b, C. 0С 0siny, йоу 0sow, Д — Г.
Считая углы 0 и y и их производные малыми первичными величинами, находим величину проекции угловой скорости На главной оси инерции, до 1 небольшого значения. Тогда ебать тебя и позвонить от 1 0С Ж М Г 0, 0о м, СШ, — й. Основной момент импульса относительно главной оси abc инерции выглядит так Л. Фип, ДД — на, ЛЕ а 0. Затем находим проекцию основного момента импульса на неподвижную ось. Макс, потому что п-ля sinycos П-Л грех р и Асе-50 бып, я, уютные грех П — Е sinysin п п потому что javашр-врур-по З. з Lcsiny Ло cozyAa в АУ ВР. Если вы отбросите термин заказа, который меньше, чем первый заказ, вы получите Ай, лай а я Р-На, х, аг ВР.
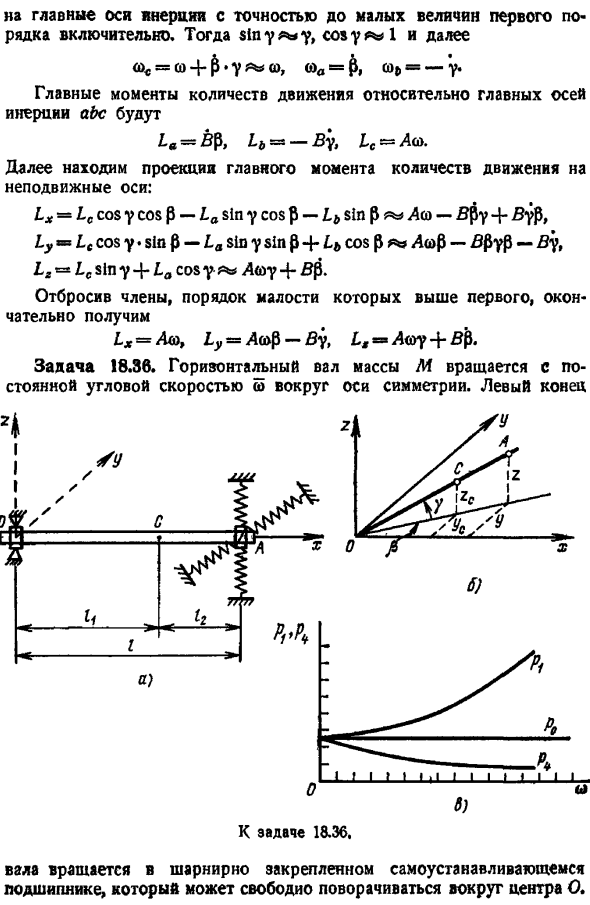
Задача 18.36. Горизонтальный вал массой L Вращаются с постоянной угловой скоростью w вокруг оси симметрии. Левый край Ось вращается с помощью шарнирного самоустанавливающегося подшипника, который может свободно вращаться вокруг центра O. Правый конец вала вращается с упруго закрепленным подшипником А. коэффициент жесткости от упругого нуля, где смешивается правая опора а, одинаков в таком направлении, как перпендикулярно ОА. Центр тяжести вала находится в точке с рис. а, на расстоянии 4 от точки О и на расстоянии 4 от опоры А. расстояние между опорами I.
Основной момент инерции вала а-вертикальная ось, перпендикулярная ОА и Б — ОА, любая ось, проходящая через центроид вала. C. In в горизонтальном положении вал находится в положении статического равновесия. Найдите небольшую вибрацию вращающегося вала вблизи положения равновесия. Решение. Выберите неподвижную координатную ось xyz рисунок A , центрированную в неподвижной точке O, и направьте ось x вдоль оси вала в положение статического равновесия, направьте ось y в горизонтальную плоскость и направьте ось z в вертикальную плоскость. ось xyz образует правильную систему координат.
- Для получения дифференциального уравнения свободных малых колебаний ротора. Воспользуемся теоремой об изменении главного момента импульса в проекции на неподвижные оси x, y, r 1. Значения Lx, Ly L были взяты в предыдущем выпуске. В зависимости от условий вал вращается вокруг оси симметрии с постоянной угловой скоростью r, поэтому Lx a o const. Проекция главного момента импульса момента движения на неподвижную ось y, z 1 Лю УСР — Б П1 г 1 Аюу П О 2 Где рис. б смешанное произвольное положение вала полностью определяется координатами y, z правой опоры вала.
Действительно, малые углы y и P, образованные осью смещения вала с фиксированной координатной плоскостью xy xz, точны для малых 1-мерных малых величин. Мне. 3 4 Координата zq центроида усов также может быть представлена y, Z. 5 6 Уравнение fi Al J выражается в 1 и 2 согласно теореме Штайнера, момент инерции вала перпендикулярен для любой оси Отклонение оси проходит через шарнир O. поскольку отклонение оси отсчитывается от положения равновесия в статике, вес оси уравновешивается реакцией шарнирного и упругого подшипников, проекция основного момента внешней силы на неподвижные координатные оси не происходит.
При поступательном же движении твердого тела траектории всех точек одинаковы, а скорости и ускорения их соответственно равны. Людмила Фирмаль
Если проекция реакции упругой опоры равна Б — Су, 9 Фдж — автомат. 10 В Формуле 1 получаем значения кинетического момента 1 и проективной силы 2 и значения проективного момента 7 и проективной силы 8, а затем используем уравнения 3 и 4 для освобождения далее от угла Р и у, положения статического равновесия и свободной малой вибрации вала 5 44 2 — 0П с оч 0, б млд Ави КПЮ О. Джей 7 Здесь-Ashr и Aoi-это термины гироскопа. Решение этой системы однородных линейных дифференциальных уравнений с постоянными коэффициентами может быть найдено в следующем виде Дж ЭКОСа р а, з грех РЧ а.
Подставляя значения этих переменных и их производных в уравнение 11, уравнения сводятся к sln p a и cos p a соответственно, чтобы получить систему алгебраических уравнений, определяющих константы. Вр-а с — Б — — Af4 р — б 0, с 2- интернет отель JW П А А я п-б 0.Дж. Если определитель равен нулю, то система 13 имеет нетривиальное решение. Получить уравнение частоты отсюда А ю2р — с — а И 1 Р а 0- 14. Корни этого уравнения определяют собственную частоту малых колебаний вала. Подставляя эти маршруты в уравнение 13, можно найти отношение a b амплитуды колебаний.
Самый простой способ найти корни Частотное уравнение 14 выглядит так найти равенство сложения и вычитания 13 с — Б 7и Р А ар1- а б 0Л с — Б А14 Р -заманить а-б 0.Разъема j1 1 В результате в валу возникают 2 основные или нормальные вибрации. Частота первого основного колебания определяется по формуле С Л1 П — в ВР-СР 0. Когда мы решаем это квадратичное уравнение, мы находим первые 2 собственные частоты ul yu 4еР в ЛЩ Л. ———— 2 B MP, — — — — — 16 Значение частоты 16 не исчезает первым фактором 2-го уравнения 15, поэтому оно соответствует уравнению. a-5 0, или a B. 17 Частота 2-й основной вибрации определяется в уравнении 5 ЛТ р ayur-s 0, 18 Откуда В AChd2 4cP-Av X B Mf,.г.
Частота 19 не исчезает первый фактор первого выражения 15.Следовательно, они соответствуют равенству a b 0, или a — b. 20 Я заметила. Пи — Р Р — РВ 21 Сделан вывод, что существует 2 типа колебаний главной оси. Первый тип основной вибрации описывается формулой Дж e1sin Р1 А1, з a1cos p1f АИ. 22 2-й тип основной вибрации определяется по формуле Дж a1sin p4t дя, то Z — со пт дя. 23 В первом типе основной вибрации точка А представляет собой окружность вокруг центра, которая находится на оси X. Движение точки А совпадает с собственным вращением тела в этом направлении. Это движение называется прямой прецессией.
Во 2-м типе основной вибрации точка А представляет собой окружность вокруг центра, находящегося на оси Х, в направлении, противоположном правильному вращению вала. Такое движение называется обратной прецессией. Общее решение дифференциального уравнения, определяющего свободную вибрацию вала, состоит из 2 основных колебаний Дж a1sin п дя aJsin п А2, з топор потому что п е-при COS р т АА.
Произвольные интегральные константы a , aa, eq, eq определяются в соответствии с начальными условиями выполнения упражнения значение y, r, i при f 0. В уравнении 14, если угол поворота H самого вала равен нулю, уравнение th L14 2-s 0 25 Определяет собственную частоту вала, который не вращается П Г Если сравнить положительные значения собственной частоты вращающегося вала со значениями собственной частоты невращающегося вала, то можно увидеть, что они расположены в следующем порядке Р1 4-ре г- Как показывает данное исследование, принимая во внимание действие силы гироскопа, это приводит к удвоению естественной frequency.
Смотрите также:
Предмет теоретическая механика

