Оглавление:




Влияние эксцентриситета приложения сжимающей силы и начальной кривизны стержня.
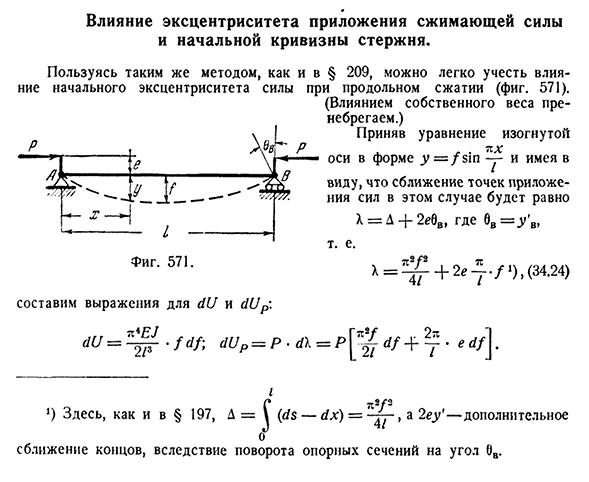
- Влияние эксцентриситета на силу сжатия и начальную кривизну стержня. Используя тот же метод, что и § 209, легко учесть влияние начального эксцентриситета силы при продольном сжатии (фиг. 571). (Мы игнорируем влияние нашего веса. Возьмем уравнение кривой оси в виде Y= / s i n—、 давайте сделаем представление DU и dUp. \
Сходимость точек приложения сил в этом случае предполагается равной X=D -| — 2e0b. Х=^+2е г. /’),(3 4.2 4 ) дю=^—Ф Д Ф — = * Е Р Ф/]. Я С 7ти2 / 3 ) Здесь, как и в§ 197, D=i(ds-dx) — >b2eu’ — add Около 7 Из-за сближения концов угол поворота опоры равен 0B.§ 2 1 0] эффект эксцентриситета приложения сжимающей силы 6 5 9 Из равенства dU=dUp находим величину наибольшего отклонения: 4E P1 Р К = равная сила-в зависимости от прогиба стержня можно найти (34.25))
Где P K-уравнение Эйлера возрастающей силы P (34.25). Установлено, что Людмила Фирмаль
при приближении силы р к критическому значению, полученному для прямого стержня, прогиб стержня быстро увеличивается, что приводит к быстрому увеличению напряжения. Поэтому наличие эксцентриситета не отражается на величине разрушающей силы в продольном направлении сжатия стержня, считается, что пока это явление происходит в пределах упругого диапазона. Поэтому это испытание на устойчивость является только испытанием
на прочность, чрезвычайно важным p, а не сжимающим совместное действие сжимающего и изгибающего момента P (E—Y), можно получить более высокое испытание на прочность. Он может быть полностью близок к начальной малой кривизне стержня (рис. 572). Уравнение оси стержня перед приложением силы эксцентриком е, стержень получает дополнительную кривизну, которую мы можем принять: г — (ф+г о) грех. И в этом случае он остается в силе. При оценке воздействия учитывалось, как мы — (обычно очень сжато Берем: г после того- Y = u0 грех (34.26) Потенциальная энергия изгиба
- балки определяется этой дополнительной кривизной и становится равной, как и в предыдущем случае, 4/ ’7′ Сближение концов криволинейных стержней после приложения силы Р выражается формулой Изменяя криволинейную ось и построив уравнение dU=dUp , Получать: v’E J f d f f. — 2Z3 dUp=P d D=(f+j-o) d/; 6 6 0 более сложные вопросы теста стабильности[глава XXX1V И так оно и есть. Р Дж е Дж ФД ФД2Z3 2z паза (/+U вых) # И. РУО г т ПК — £1 Р Р К (34.27) Таким образом, уравнение кривой оси является、: Около Р УО р г К. Р + УО. K H Грех —. Икс Горе грех» » г» К ’ (34.28)) То есть максимальное значение на момент приема: * Единое время Uounit (34.29)) Как и в предыдущем случае, отклонение резко возрастает только
с приближением R к Rk. Таким образом, при пропорциональном напряжении эксцентриситет и начальная кривизна также основаны на теоретическом рассмотрении, которое не влияет на величину разрушающей силы при продольном сжатии стержня. Он отличается от малого и среднего полюса гибкости. При критических напряжениях, выходящих за пределы пропорциональности, обе эти ситуации существенно снижают значение АК. Это показано экспериментами и подтверждено теоретическими попытками расчета величины критической деформации. Что касается стержней средней гибкости, то из эксперимента видно, что влияние эксцентриситета очень важно и влияет на устойчивость длинных стержней, но в гораздо меньшей степени.
Дополнительные косвенные эффекты, исследуемые в этом пункте, заключаются в увеличении предельной скорости перехода к среднему и малому изгибам, а такж Людмила Фирмаль
е в оценке влияния эксцентриситета и начальной кривизны на прочность и устойчивость сжимаемых стержней, несколько превышающих предел прочности, необходимо учитывать численные значения E и Y. В тщательно изготовленном стержне можно ожидать, что начальное отклонение d’o будет по крайней мере в длину; при менее тщательном изготовлении lUvU U будет по крайней мере в два раза больше длины. Хороший эксцентриситет центрирования можно оценить в 1/750 длины. Кроме того, необходимо учитывать допуски на размеры сечения; их можно считать эквивалентными исходной стрелке того же размера, что и эксцентриситет L/40. Здесь h-размер поперечного сечения в плоскости возможной потери устойчивости. Для составного
сечения следует иметь в виду дополнительный эксцентриситет приблизительно y/960 из-за возможных различий в площади отдельных ветвей стержня (§ 211).J обоснование расчета § 2 1 1 соединительная сетка 661 Таким образом, для стержня с непрерывным поперечным сечением считаются возможными следующие минимумы e и _u0: _ J_f A_ _ I, h e750 * 40 и 1000 ″ N o * Помимо эксцентриситета и начальной кривизны, всегда возможны на практике многие ситуации, которые оказывают гораздо более сильное влияние на несущую способность компрессионного стержня, чем на прочность балки или удлиненной детали. Для стальных конструкций влияние этих дополнительных обстоятельств учитывается увеличением части коэффициента безопасности (10-20%) на устойчивость (см.§ 204).
Смотрите также:

