Контрольная работа Д4.
Вертикальный вид длинной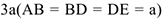 
, Закрепленный подпятником 
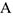и подшипником 
(рис. Д4,а), вращается с постоянной угловой скоростью 
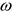. К валу жестко прикреплен в точке 
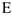ломанный однородный стержень массой 
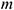и длинной 
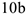, состоящий из двух частей 1 и 2, а в точке 
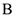прикреплен невесомый стержень длинной 
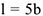с точечной массой 
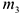на конце; оба стержня лежат в одной плоскости.
Дано:
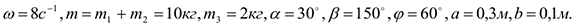
Определить: реакции подпятника 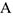и подшипника , пренебрегая весом вала.
Решение.
Изображаем (с учетом заданных углов) вал и прикрепленные к нему в точках 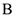и 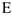стержни (рис. Д4,б). Массы и веса частей 1 и 2 ломанного стержня пропорциональны длинам этих частей и соответственно равны
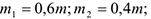
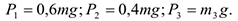
Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси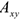 
так, чтобы стержни лежали в плоскости 
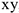, и изобразим действующие на систему силы: активные силы — силы тяжести 
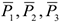и реакции связей составляющие реакции подпятника 
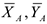и реакцию цилиндрического подшипника 
.
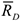Согласно принципу Даламбера, присоединим к этим силам силы инерции элементов однородного ломанного стержня и груза, считая его материальной точкой.
Так как вал вращается равномерно, то элементы стержня имеют только нормальные ускорения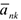 
, направленные к оси вращения, а численно 
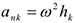, где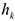 
— расстояние элементов от оси вращения. Тогда силы инерции 
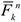будут направлены от оси вращения, а численно 
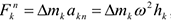, где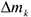 
— масса элемента. Так как все 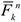пропорционально 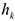, то эпюры этих параллельных сил инерции стержня образуют для части 1 треугольник, а для части 2 — прямоугольник (рис. Д4,б).
Каждую из полученных систем параллельных сил инерции заменим ее равнодействующей, равной главному вектору этих сил. Так как модуль главного вектора сил инерции любого тела имеет значение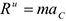 
, где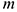 
— масса тела, 
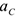— ускорение его центра масс, то для частей стержня соответственно получим
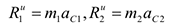
Сила инерции точечной массы 3 должна быть направлена в сторону, противоположную ее ускорению и численно будет равна
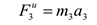
Ускорения центров масс частей 1 и 2 стержня и груза 3 равны:
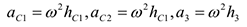
Где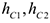 
— расстояния центров масс частей стержня от оси вращения, а 
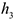— соответствующие расстояния груза:
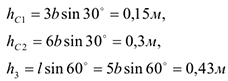
Подставив в (2) и (3) значения (4) и учтя (5), получим числовые значения 
и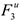 
:
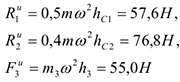
При этом линии действия равнодействующих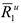 
и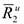 
пройдут через центры тяжестей соответствующих эпюр сил инерции. Так, линия действия 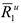проходит на расстоянии 
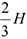от вершины треугольника 
, где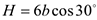 
.
Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим для этой системы сил три уравнения равновесия. Получим
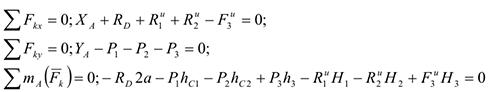
Где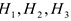 
— плечи сил 
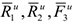относительно точки 
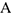, равные (при подсчетах учтено, что 
).
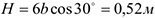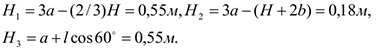
Подставив в уравнения (7) соответствующие величины из равенств (1), (5), (6), (8) и решив эту систему уравнений (7), найдем искомые реакции.
Ответ:
