Оглавление:
Найдем вероятность того, что отклонения относительной частоты 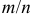 от постоянной вероятности
от постоянной вероятности 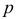 по абсолютной величине не превышает заданного числа
по абсолютной величине не превышает заданного числа 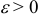 , т.е. найдем вероятность того, что осуществляется неравенство:
, т.е. найдем вероятность того, что осуществляется неравенство:
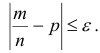
Раскроем модуль 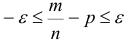 или
или 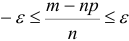 . Умножим эти неравенства на множитель
. Умножим эти неравенства на множитель 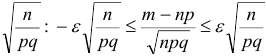 .
.
Используя теорему Лапласа, получим:
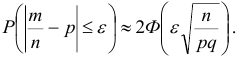
Пример №1
Вероятность появления события в каждом из 10000 независимых испытаний 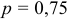 . Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,001.
. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,001.
Решение:
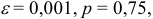
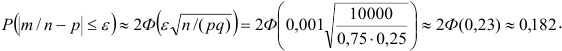
Пример №2
Сколько раз надо бросить монету, чтобы с вероятностью 0,6 можно было ожидать, что отклонение относительной частоты появлений герба от вероятности 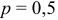 окажется по абсолютной величине не более 0,01?
окажется по абсолютной величине не более 0,01?
Решение:
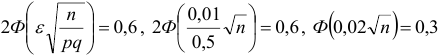 . По таблице находим
. По таблице находим 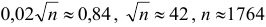 раза.
раза.
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:

