Верхние и нижние суммы Дарбу. Верхний и нижний интегралы Дарбу

Верхние и нижние суммы Дарбу. Верхний и нижний интегралы Дарбу

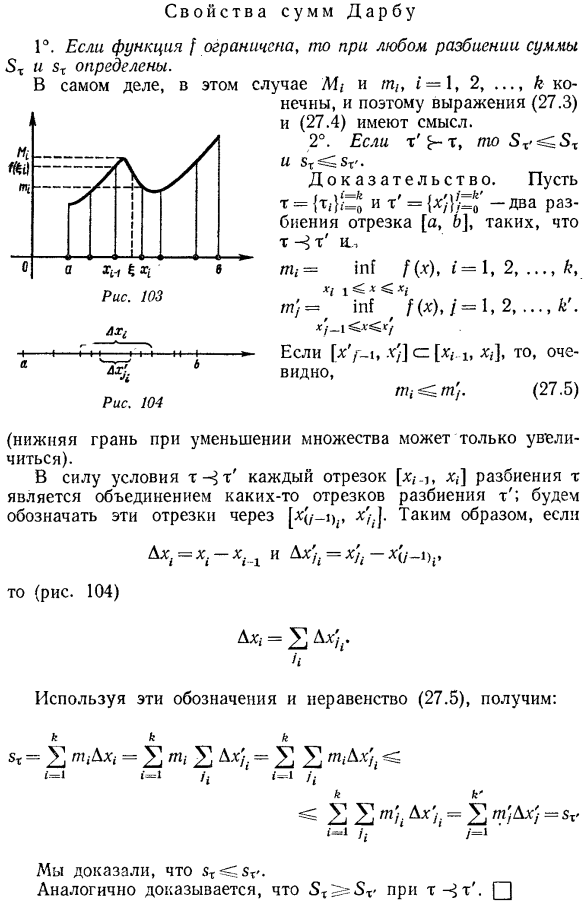
Верхние и нижние суммы Дарбу. Верхний и нижний интегралы Дарбу. Определите функцию f (x) с интервалом[a, b], где m = {x;} {=ее разбиение, а Ax,= x, x,, r = 1, 2,.. 。, Настройки (рис. 103） Очевидно, 5х = ^ 5х. Сумма 5X называется суммой верхнего предела, а 5X-суммой Нижнего дарбокса. Суммы дарбу свойства 1°. Фактически, в этом случае Л4, и т1= 1, 2、 Диаграмма 104 Поскольку она не конечна, выражения (27.3) и (27.4) имеют смысл.

Если функция ограничена, то для любого раздела определяются в общей сложности Sx и sx. Людмила Фирмаль

• Доказательство. м = {м,•}!■= И m ’= {x)} E) ’ это 2 разбиения отрезков [a, b] и m-тm ’ [Y / −1, x)] Если a [x1A, x.], очевидно (Нижний предел при уменьшении набора может быть только увеличен). Из-за условия m> m каждый сегмент m[x(_x, x]]является объединением нескольких сегментов m. эти сегменты[(/-1);, x).он представлен [].So … Используя эти обозначения и неравенства (27.5), вы получаете: 5X = ^ 5X’ доказано, что Аналогично, мы можем доказать, что M > M ’ равно 5X2 = 5X.] В результате плиткой двойки и интервалы [а, 6]м2, неравенство 5T1 ^ 5T2(27.6） То есть нижний предел суммы Дарбу меньше верхнего предела.

• Фактически, учитывая 2 раздела xx и m2 сегментов [a, b], будут существовать разделы m этого сегмента, такие как tr-bx и m p-m2 (см.§ 27.1). Используя свойство 2°、 Очевидно, что суммы Римана и Дарбо связаны неравенствами Следующие свойства являются улучшенной версией этого оператора. 3°. бык =σ(Ф; НХ,…если, μ) интегральная сумма Римана, соответствующая данному разбиению m、 Доказательство. m =разбиение сегментов Набор чисел X, -, I = 1, 2,…константа K и AR 0, 1 = 1, 2,…если, к, то X = / x. x = 2a, X;, e X/, r = 1, 2,…легко видеть, что уравнение k выполняется(почему?） К. ЗІР х = ^ а, ЗІР х,, 1нг х = 2 сбн, 1нг х, -.

Из характеристик суммы Дарбу 1°и 2°, если функция f ограничена, то как Интеграл Дарбу, так и верхний под ним являются конечными. Людмила Фирмаль

• С этим мы справились. Точно так же Интервал[x, _1, x, -] (см. раздел 19.6), 1 = 1, 2,…. К Доказательство. Во-первых, для данного 2 набора чисел X и Y、 Тогда Zir 2 = Zir X-t! В(почему?） Используя это、 И так оно и есть.、 Вставь его сейчас же. / * = zir5x, / * = тг 5х. / *Называется нижним интегралом дарбу от / в интервале[a, b], а/ * его верхним интегралом. By свойство 2°последствия.

Смотрите также:

Предмет математический анализ

Определение интеграла по Риману.	Необходимые и достаточные условия интегрируемости.
Ограниченность интегрируемой функции.	Интегрируемость непрерывных и монотонных функций.