Велосипед

Оглавление:

Велосипед

Из интересного исследования Бурле Bou r let, Traite des bicycletts et bicyclettes, Gauthier Villars мы заимствуем следующее применение теории относительного равновесия: основная часть велосипеда, к которой крепятся все остальные, представляет собой раму, обычно выполненную в виде жесткого пятиугольника RQE S рис.251. Ось колеса L закреплена в точке R за рамой, а передняя часть рамы снабжена втулкой EI, через которую проходит рулевое колесо. Рулевое колесо оснащено вилкой B в нижней части, через которую проходит ведущее колесо D, а его ось закреплена на вилке в точке B.

Верхний руль представляет собой почти горизонтальную G трубку, которая заканчивается 2 ручками, которые велосипедист держит в руке. Велосипедист сидит в седле S, прикрепленном к средней верхней части рамы. Рама станка представляет собой плоскость симметрии, включающую втулку Е1 рис. 251. Л g ы Рис. 251а. Центр седла s и центр колеса G R. эта плоскость называется центральной плоскостью. Плоскость колеса называется плоскостью, перпендикулярной центру этого колеса. Плоскость задних колес всегда совпадает с центральной плоскостью, а плоскость рулевого колеса меняет свое положение относительно центральной плоскости, и если она совпадает с ней, то оба руля равноудалены от центральной плоскости.

Но он мог бы, прыгнув без начальной угловой скорости, тоже заставить себя повернуться на некоторый угол в пространстве. Людмила Фирмаль

Можно проигнорировать как первое приближение. Точка соприкосновения обоих колес с землей обозначается буквой a n B. предположим, что ось x рулевой трубки проходит через контакт B рулевого колеса wheel. In в этом случае точка B будет фиксированной точкой на средней плоскости, а линия AB будет определенной длины, независимо от положения рулевого управления wheel. It предполагается, что эта прямая АВ контактирует с задними колесами, является пересечением промежуточной плоскости с землей, а земля является flat. It также предполагается, что велосипедист не двигается вместе со своим телом, а сидит так, что плоскость симметрии тела совпадает с центральной плоскостью.

В этих условиях центроид велосипедиста и велосипеда G рис. 251а почти наверняка является неподвижной точкой на midplane. So, основание с перпендикуляра, которое опускается от центра тяжести к прямой АВ, является неподвижной точкой на этой прямой. Во первых, выясните, что такое след колеса на Земле, если мы предположим, что рулевое колесо образует определенный угол со средней плоскостью. Разровняйте почву и перенесите ее на плоскость рисунка.

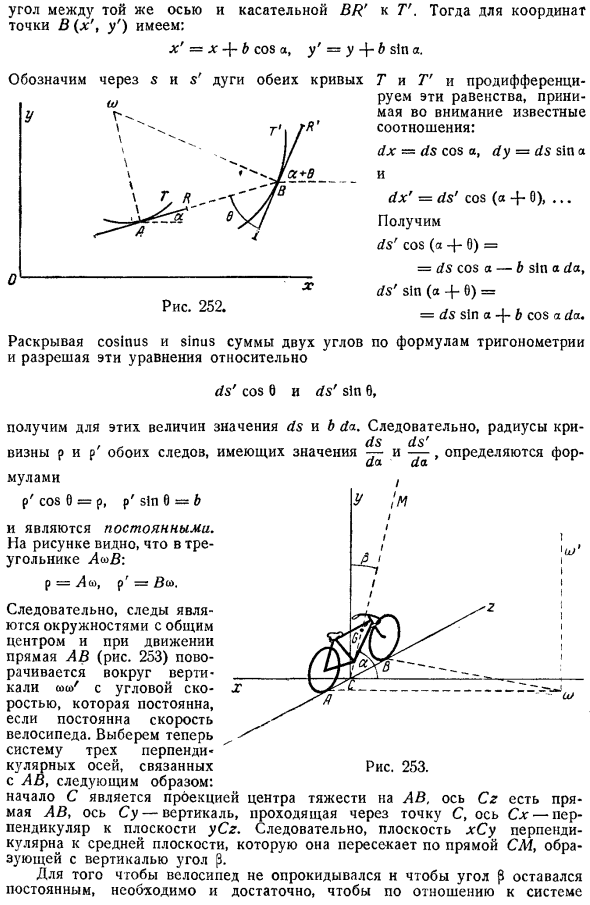
A и B точки соприкосновения между задним колесом и направляющим колесом, а AR и BR прямые пересечения между плоскостью и землей обоих колес. wheels. In в этом случае AR будет соответствовать AB в направлении рис. 252. Если наклон центральной плоскости относительно вертикали остается постоянным, то угол 0 между BR и AB остается постоянным. Прямые AR и BR почти не отличаются от касательных трека T и T колес на земле. Вы можете видеть, что эти следы представляют собой 2 круга с общим центром к точкам, которые находятся на пересечении нормалей следов обеих точек A и B.

Факт, так как x, y координаты точки A, А b угол касательной AB к T для длины AB, фиксированной оси Ox, то угол через a 0 это угол между той же осью и касательной BR к T .Тогда координаты точки B x , y выглядят следующим образом: x = X4 cos a, y = y 4 тонкий A. Т и Т. Мы выделяем эти уравнения с учетом известных соотношений. ДХ = ДС потому что, dу = ДС грех и ДХ ДС, потому что а 4 0 ДС, потому что а 4 0 = = ДС, потому что в грехе да, ДС грех 4 0 = = ДС грех 4 Б потому что да. Косинус и синус в уравнении тригонометрии показывают сумму 2 углов, и эти уравнения ДС cos0 и DS грех о Для этих величин получите значения ds и B da.

Следовательно, радиус Виза И и Р обоих следов со значением определяются выражением. p COS 0 = p, p Sin 0 b И он является постоянным. На рисунке показан треугольник Lo B. п = со, п= БВ. Итак, трасса представляет собой круг с общим центром, а при движении прямая линия АВ рис.253 вращается вокруг сои. Если скорость велосипеда постоянна, то угловая скорость постоянна. Выберите систему с 3 вертикальными осями, связанными с AB, следующим образом: Начало C является проекцией центра тяжести АВ. Ось Cz представляет собой прямую линию AB, ось Cy вертикальную линию, проходящую через точку C, а ось Cx перпендикулярна оси yCr plane.

В результате плоскость xCy перпендикулярна центральной плоскости, пересекается с прямой линией CM, образуя вертикальную линию и угловую окружность. Необходимо и достаточно, чтобы существовало относительное равновесие относительно системы валов Cshyz для предотвращения опрокидывания велосипеда и поддержания постоянного угла 8.Но движение этих осей есть вращение с постоянной угловой скоростью со всего света vertical. It предполагается, что масса колеса очень мала по сравнению с общей массой и равна zero.

Также игнорирует движения ног. Это предполагает, что он не будет двигаться в середине position. To выразив, что существует относительное равновесие, необходимо написать, что существует равновесие между реакцией грунта, гравитацией и центробежными силами. Результат гравитации равен весу GP = Mg рис.

В этом примере человек обладает начальной угловой скоростью, которую он увеличивает при помощи внутренних сил. Людмила Фирмаль

Приложена центробежная сила, которая грубо суммируется к точке G, и направлена к оси вращения вдоль вертикали G g MV И MTO GG , или равный 5—.Где V обозначает скорость точки G, а тушеное мясо Радиус окружности, описываемой этой точкой GG. Берл обосновывает это приближение, основываясь на замечаниях, сделанных в 421.По соображениям симметрии ось GC является почти инерциальной главной осью центра тяжести. Угол Р, образующий вертикальную линию через ось GC и точку G, обычно невелик, и эта вертикальная линия почти совпадает с главной осью инерции. Таким образом, можно предположить, что линия, проведенная из точки G параллельно оси вращения ww, является почти инерционной осью точки G.

Это позволяет применить замечания, сделанные в разделе 421. Затем исключить реакцию почвы Сумма моментов сил T и P относительно оси АВ равен нулю. Для этого достаточно спроецировать силы P и T на xCy плоскости, перпендикулярной к Ab, по определению данный момент, и брать моменты этих проекций относительно точки С. проекция силы тяжести Р равна стоимости всей силы. Проекцией Силы F является горизонтальная сила Fn, равная cos .Где обозначает угол FGFb, образующий прямую FGG с проекцией F GG на плоскость yCx. Ф cos cos = Р грех. Проекция треугольника GG G на горизонтальную плоскость равна тому же треугольнику. Равна P, мы равны переменного тока, то есть известной постоянной длиной c.

Затем, для sin , мы получаем значение и уравнения равновесия. Л4 П2 Если в нем вы заменили F и P на их значения и Mg, то он принимает вид: В общем случае R очень велик по сравнению с размером машины, и вы можете игнорировать это значение. И затем… U2 Если предположить, что радиус R очень велик и указанное приближение приемлемо, то полученное относительное равновесие становится неустойчивым. Дело в том, что при наклоне велосипеда к Земле угол 3 увеличивается, момент веса увеличивается, момент силы F уменьшается, первый момент больше 2 го момента, а угол Р дальше increased. In чтобы не упасть, велосипедист должен повернуть руль в сторону поворота, чтобы увеличить угол.

Затем точка перемещается, Leo, Vsh, R уменьшается и центрифугируется mV2. сила r = увеличивается и преодолевает гравитацию. если P уменьшается Затем происходит обратное явление. Если боковое трение скольжения грунта неограниченно, то условия относительного равновесия достаточны. Но пусть коэффициент трения имеет определенное значение. в относительном равновесии результирующие силы P и Px пересекают ось AB, образуя вертикальную линию и угол p. To предотвратите его от смещать Это неравенство указывает на то, что при заданной скорости невозможно описать круг с радиусом меньшим, чем радиус скользкой почвы.

Чтобы описать окружность с заданным радиусом R, нам нужно использовать предыдущие неравенства babout и r 1 e t, loc. citn п. Этого достаточно, чтобы замедлить движение навстречу 26 27. Чтобы ознакомиться с теорией велосипедов, наградами являются работы Бурле Bulletin de la Socidte mathematique, 1899 и работы Карвалло Carvallo, Journal de i Ecole Polytechnique, Ve etVIe.

Относительное движение и равновесие системы. Пример относительного движения	Относительное равновесие на поверхности Земли
Твердое тело	Относительное движение на поверхности Земли

Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.