Оглавление:

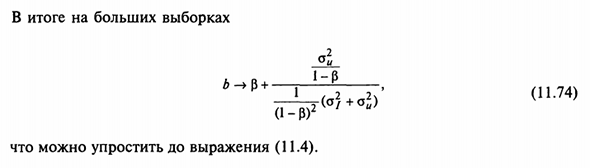

Величина смещения оценки для одновременных уравнений
- Расчетное значение смещения уравнений одновременного Смещать оценки при оценке моделей по уравнениям одновременности С помощью OLS нет четкой формулы. Она всегда Определяется структурой модели. Здесь мы рассмотрим случай смещения Чай при использовании уравнений регрессии.
- Приведены параметры функции потребления. Как показано в разделе 3.1, оценка с использованием OLS может занять некоторое время. Два составляющих бита: истинное значение коэффициента и ошибка: , Cov (y, C) a Cov (Y, u) * = «W) P + W) * <1 L 7 0> Я хочу найти математическое ожидание б.
К сожалению не могу Cov (Y, w) / Var (Y) — это отношение двух, поэтому сделать это напрямую. Людмила Фирмаль
Маскирует каждую частично зависимую от одной и той же случайной Пояс. Значение Cov (Y, u) напрямую зависит от и. Значение переменной (Y) Поскольку Y также частично определяется и, это также зависит от и. В то же время, если большая выборка принимает определенные допущения Genius Cov (Y, u) и Var (Y) стремятся к общему населению Ност поп. cov (Y, and) и поп.
- Соотношение var (Y) и Cov (Y, u) / Var (Y) равно КОЮ / G2Y. (11.3) можно использовать для выражения aYu как sui = pop.cov 1-P 1-1 * n- = popxov | ^, wJ + pop.cov | -j ^ p, wj> (11.71) Термин os / (1-p) исчезает, потому что он является константой. Без причины Предположим, что сумма инвестиций коррелирует со случайным компонентом Расход, и не зря, мы можем предположить.
Население cov (/, и) = 0. В результате: «1 1 2 OUI = pop.covj-, * / f = j ^ Ou- (11,72) Опять же, термин a / (1-p) удаляется как константа, и pop принимается. cov (/, u) = 0, Он получает: 2 {со мной Среднее = поп. ван-1- р- 1- + -п- 1- + р 1 (1-P) 2 [pop.var (/) + pop.var (w) + 2pop.cov (/, w)] = (1-RC- (° / + <**)) • (11> 73) 348 В результате для больших образцов <А В! -Р P _ L _ ^ 2 _ 2 / (11,74) (1-р) Можно упростить до уравнения (11.4)
Кроме того, если большая выборка Var (/) имеет тенденцию быть в) Людмила Фирмаль
Смотрите также:
| Условие размерности для идентификации | Метод максимального правдоподобия (ММП) |
| Идентификация относительно стабильных зависимостей | Спецификация модели |

