Оглавление:
Векторы и операции над ними
Геометрическим вектором называется направленный отрезок, т. е. отрезок с началом и концом.
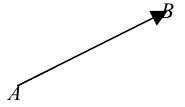
Обозначается вектор 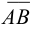 ,
,  .
.
Величиной вектора называют число, равное длине отрезка, соединяющего его начало и конец.
Нулевым вектором называется вектор, начало и конец которого совпадают. Его обозначают 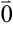 .
.
Вектор —  называется противоположным вектору
называется противоположным вектору  , если они лежат на параллельных прямых, имеют равные длины и различные направления.
, если они лежат на параллельных прямых, имеют равные длины и различные направления.
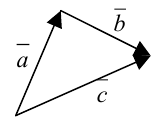
Суммой двух векторов  и
и 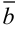 называется вектор
называется вектор 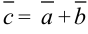 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец вектора
, а конец вектора 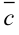 совпадает с концом вектора
совпадает с концом вектора 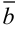 при условии, что вектор
при условии, что вектор 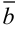 отложен от конца вектора
отложен от конца вектора  .
.
Очевидно, что
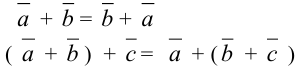
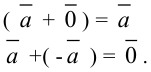
Разностью  —
—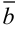 двух векторов
двух векторов  и
и 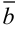 называется вектор
называется вектор 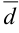 , который в сумме с вектором
, который в сумме с вектором 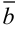 дает вектор
дает вектор  .
.
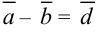 , если
, если 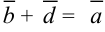 .
.
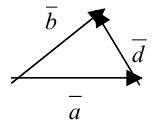
Чтобы получить разность  —
— 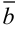 векторов
векторов  и
и 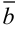 , надо отложить их из одной точки и соединить конец второго
, надо отложить их из одной точки и соединить конец второго 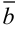 с концом первого
с концом первого  .
.
Произведением вектора  на число
на число 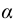 называется новый вектор
называется новый вектор 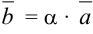 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) 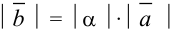 ;
;
2)  и
и 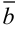 одинаково направлены при
одинаково направлены при 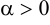 ;
;
3)  и
и 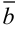 противоположно направлены при
противоположно направлены при 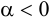 .
.
Произведение вектора на число обладает следующими свойствами:
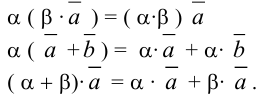
Действия над векторами, заданными своими координатами
Пусть даны два вектора: 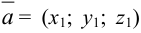 и
и 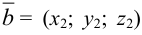 . Тогда справедливы следующие правила:
. Тогда справедливы следующие правила:
Правило сложения двух векторов:
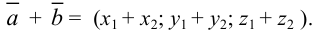
Правило вычитания двух векторов:
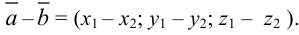
Правило умножения на число:
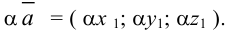
Произведение 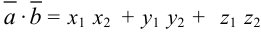 называется скалярным произведением векторов.
называется скалярным произведением векторов.
Векторы коллинеарны, если лежат на параллельных прямых или на одной прямой.
Векторы компрланарны, если лежат на одной плоскости.
Условие коллинеарности: 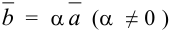 или в координатной форме это имеет вид:
или в координатной форме это имеет вид: 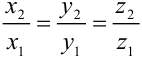 .
.
Два ненулевых вектора  и
и 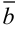 ортогональны тогда и только тогда, когда их скалярное произведение равно 0.
ортогональны тогда и только тогда, когда их скалярное произведение равно 0.
В координатной форме условие перпендикулярности имеет вид: 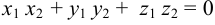 .
.
Задача №19.
При каких значениях 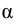 и
и 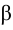 векторы
векторы 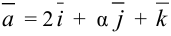 и
и 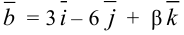 коллинеарны?
коллинеарны?
Решение:
Координаты этих векторов 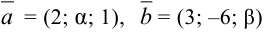 должны быть пропорциональны:
должны быть пропорциональны: 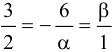 .
.
Отсюда находим, что 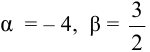 .
.
Задача №20.
При каких к векторы 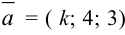 и
и 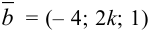 перпендикулярны?
перпендикулярны?
Решение:
Воспользуемся условием перпендикулярности:
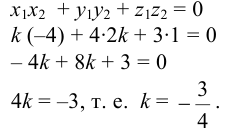
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

