Оглавление:





- Векторные и линейные операции над ними Значение, которое полностью определяется числом, называется скаляром. Примерами скалярных величин являются площадь, длина, объем, температура, работа и масса. Другие величины, такие как сила, скорость и ускорение, определяются не только числами, но и направлением. Такое количество называется вектором. Векторные величины представлены геометрически с использованием векторов. Вектор — это направленный отрезок прямой линии, то есть отрезок с определенной длиной и определенным направлением.
Вектор B A (начинается в точке B и заканчивается в точке A) называется противоположностью вектора AB. Противоположность вектора а обозначена -a. Длина или модуль вектора AB — это длина отрезка, обозначенная \ AB . Вектор нулевой длины называется нулевым вектором и обозначается нулем. Нулевой вектор не имеет направления. Вектор, длина которого равна 1, называется единичным вектором. Указано е.
Если A — начало вектора, а B — конец, вектор обозначается символом AB или a. Людмила Фирмаль
Единичный вектор, направление которого совпадает с направлением вектора а, называется единичным вектором а и обозначается а0. Векторы a и b называются коллинеарными, если они лежат на одной или параллельной линии. Написать || Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным с любым вектором. Два вектора a и 6 приравниваются (a = 5), если они коллинеарны, имеют одинаковое направление и одинаковую длину.
Из определения векторной эквивалентности вектор может передаваться параллельно самому себе,Любая точка о космосе. На следующем рисунке векторы образуют прямоугольник. Уравнение b = d выполнено, но a f c. Векторы a и c противоположны, a = -c.
| Решение систем линейных уравнений методом Гаусса | Проекция вектора на ось |
| Системы линейных однородных уравнений | Разложение вектора по ортам координатных осей. Модуль вектора направляющие косинусы |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Равные векторы также называют свободными. Три вектора в пространстве называются копланарными, если они лежат в одной или параллельных плоскостях. Если хотя бы один 0 или 2 из 3 векторов являются арнами на одной линии, такие векторы находятся в одной плоскости. Линейные векторные операции Понимать операции сложения и вычитания вектора, а также умножение числа вектора.
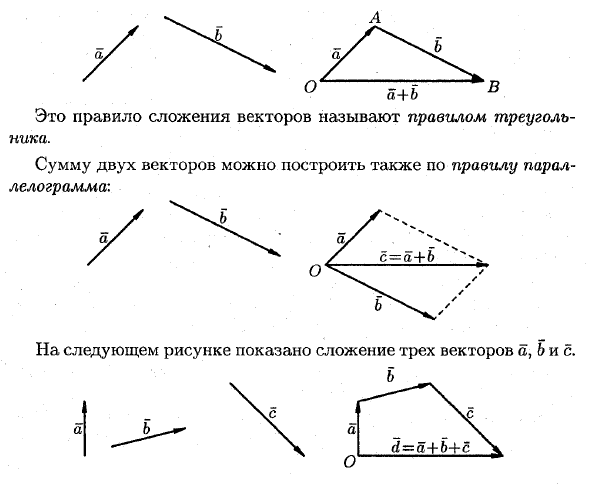
Пусть a и b два произвольных вектора. Возьмите любую точку O и создайте вектор OA = a. Из точки A отложите вектор AB = b. Вектор ОВ, который связывает начало первого вектора и конец второго вектора, называется суммой векторов o и b. OB = 4-б. Это правило сложения векторов называется правилом треугольников. Сумма двух векторов также может быть построена по правилам параллелограмма.
Сумма двух векторов также может быть построена по правилам параллелограмма. На следующем рисунке показано добавление трех векторов a, b и c.
O * -b- Это правило сложения векторов называется правилом треугольников. Людмила Фирмаль
Под разницей между векторами a и b мы понимаем вектор c = a-b, где b + c = a. Обратите внимание, что в параллелограмме, построенном с векторами a и b, диагональ в одном направлении представляет собой сумму векторов a и a, а в другом — разность. + 6 а-6 1 Вы можете вычесть вектор по правилу: a-b = a + (-6), то есть вычесть вектор, сложив векторы на другой стороне вектора a и b Произведение вектора a и скаляра (числа) A — это вектор Aa (или oA) с длиной | A |. • \ a \ на той же прямой линии, что и вектор a, имеет направление вектора a, если A> 0, и противоположное направление, если A <0.
Например, если задан вектор, векторы Za и -2a. Давайте посмотрим. ■ т и -2a Из определения векторного произведения по номеру этот продукт имеет следующие характеристики: 1) Если b = A • a, b || Наоборот, для b || a, (aφ0), A уравнение b = Aa верно. 2) Всегда a = | a | • a0, т.е. каждый вектор равен произведению модулей на orth. Векторные линейные операции имеют следующие свойства:1.d + 6 = 6 + a, 2. (a 4-6) + c = a + (6 + c), 3. Ai • (Л2 • a) = Ai • Л’2 • a, 4. (Ai + A2) • a = Aj • a 4- A2 • a, 5. A • (a + b) = A • a + A • 6. Эти свойства позволяют выполнять преобразования с линейными операциями с использованием векторов так же, как и с обычной алгеброй. Изменение термина, вставка скобок, группа, общие факторы для скаляра и вектора.

