
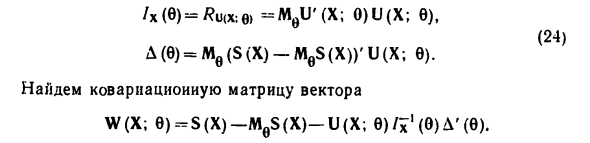

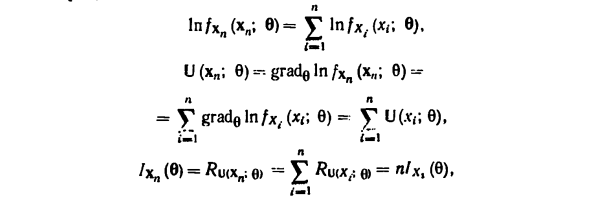

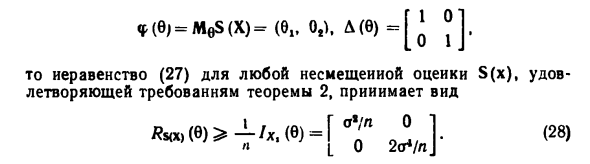


Векторный параметр
- Теорема 2. Плотность образца равна fx (x; c), c = (8i, …, 6b) ev (c — область Rk) 190 Home 0 /, / = 1; …. k, векторная статистика S (x) = (S \ (x), …, Sr (x)) Несмещенная оценка вектор-функции /? 5 (x, (c)> D (e) / x-1 (c) D (c) ‘, B2) где = [- ^ 7Φ / (в), / = 1, …, r; / = 1 фут] Полоски указывают операции транспонирования. равенство Б2) илег лесго гогья и 8 (x) = φF) + и (x; c) A (c) B3) Подмножество P ‘^ -проблемости1; A (c) — матрица kXr Полный ранг, зависит только от века. Доказательство. Подобно тому, как это делается Скалярный параметр, это легко показать MeU (X; 6) = 0, U (x; e) = град / х (x; 0), ^ WJLln / xfX; c). Ну и что хх (-) -? и (x; »-iWeU ‘(X; 0) U (X;)), B4) AF) = Me (S (X) -MflS (X)) ‘U (X; c).
Найти ковариационную матрицу вектора W (X; 6) = S (X) -MflS (X) -U (X; 6) / x ‘@) A’ (с). * Утверждение теоремы 2) дано. B2) Равенство /? Это возможно только если w = [0], то есть только в единицах повторной вероятности. S (X) -M (| S (X) -U (X; c) I-1 (c) A ‘(c) = 0, B5) Затем следует B3). да Вывод 1. Неравенство В2) Равенство, A (c) является обратимым, D-MB). / h’f). φ (с) непрерывна в 9. Тогда существуют функции / (()), …, Г)), B (c), K (x). / x (x; c) = exp j jr Ht (c) S, (x) 4 — @@) fK (x) j. B6) 1-1 То есть статистическая модель является экспоненциальной. Действительно, из B3) вектор градиента Оценка 1n / (: c) = S (x) A-1 @) — q: (c) A-1 @)
Смотри сноску к р. 182. 191 После базовой конвертации, учтите Б4) tfw = Me (S — MeS — U / -1A ‘)’ (S — MeS — и / — ‘D’) = Людмила Фирмаль
Функция ln / (x; c) -потому что она непрерывно зависит от 0 Дифференцируемая функция не временных переменных = (in |, …. vp) в области Площадь в. В ходе математического анализа В этом случае в In / (x; b) -In / (x; bn) -: | «(S (x) A до 1 (b) — (p (b) A-1 (b)) dV, Где интеграл кривой взят вдоль любой гладкости Путь, соединяющий точку с 0, d \ — Элемент пути вектора, dash, указывает на транспонирование. Интегрируя, вы получите выражение B6). Следствие 2. Когда X является независимым повторяющимся случайным Тогда выборка 1n / XA (xn; 9) =? 1n / x, ( G.c), U (xn; e) -градельн / xn (xfI; c) = Y класс In / X / (ад c) -f U (v ‘; c)> N „(C) =? И (X„; c) «- =
И неравенство Б2) Rsix) (c)> — A (c) / *, ‘(c) A (c)’ B7) Я Давайте рассмотрим пример. (III) Повторение независимой выборки из распределения Положим N (μ, σ2) 9i = | i, 62 = σ2. тогда N Ох; 6) = [V ^ Ttr Major Rd имеет общую поддержку-R всего пространства Требование дифференцируемости интеграла теоремы выполнено Теорема 2. Найти — ^ «M * ;; c) = ^ — (_ 1„ /-Lme.-JLfc-e,) ‘) — Откуда вектор U (xi, 6) и симметричная матрица 11 ‘(xi 0) X получить выражение f / (i; c) U (lu, c) = ((. V, -6,) 0 ^ -1 (.vt-OO ^ -vG1), u ‘(xV 0) u (.vi; c) J «ГЧ * | — *.)’ W.-ej ‘- ^ — ejo ^ l Вот так G | (C) = A \ u ‘(X1,9) U (A ;; c) <| G OT1 0 Около 20F Здесь мы использовали следующее соотношение для стандарта
- Нормальная еда с. | — (Xi-6i) / «-1’2 (см. § 7, подраздел 3): M> V = 0, MU | 4 = 3. с того времени = @lt 02), L (c) [Про идж- Несмещенная оценка S (x), удовлетворяющая неравенству B7) Форма, отвечающая требованиям теоремы 2, имеет вид B8) 193 особенно D5, (X)> o2 / n, D52 (X)> 2VVt. Лучшее смещение Я S, (л.с.) -7 — V xt. Si (x „) = — 1 = 1 № Ясно удовлетворить требования регулярности теоремы 2 и Их ковариационная матрица О я O 2a4 / («-I) J Когда используются X и 2 = V (X и -XJ независимы, я = я Распределение aTlZ является V. \ — \, то есть oT’Z n — 1 независимая сумма N в квадрате, 1). с. сравнить Видно, что нижний предел достигнут в B8), B9) и 02.
Однако, если n большое, разница незначительна. Людмила Фирмаль
Смотрите также:
| Информация по Фишеру | Границы дисперсии при нарушении условий регулярности |
| Скалярный параметр | Функция правдоподобия |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.
