Скалярным полем называется область, расположенная в плоскости или пространстве, с каждой точкой 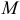 которой связано определенное значение некоторой скалярной физической величины
которой связано определенное значение некоторой скалярной физической величины 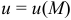 .
.
Функция 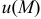 , определяющая плоское скалярное поле, зависит от двух переменных
, определяющая плоское скалярное поле, зависит от двух переменных 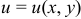 , а функция, определяющая пространственное скалярное поле, зависит от трех переменных
, а функция, определяющая пространственное скалярное поле, зависит от трех переменных 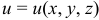 .
.
Линией уровня плоского скалярного поля называется совокупность точек плоскости, в которых функция этого поля имеет одинаковые значения. Линия уровня определяется уравнением 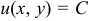 . Различным постоянным значениям
. Различным постоянным значениям 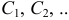 функции поля соответствуют различные линии уровня:
функции поля соответствуют различные линии уровня: 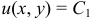 ,
, 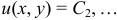
Поверхностью уровня пространственного скалярного поля называется совокупность точек пространства, в которых функция этого поля имеет одинаковые значения. Поверхность уровня определяется уравнением 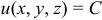 .
.
Через каждую точку проходит только одна поверхность (линия) уровня. Они заполняют всю рассматриваемую область и не пересекаются между собой.
Векторным полем называется плоская или пространственная область, с каждой точкой 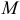 которой связано определенное значение некоторой векторной физической величины
которой связано определенное значение некоторой векторной физической величины 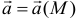 .
.
Если векторное поле отнесено к прямоугольной системе координат 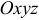 , то вектор
, то вектор 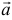 будет векторной функцией, а его проекции
будет векторной функцией, а его проекции 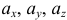 на оси координат будут скалярными функциями от переменных
на оси координат будут скалярными функциями от переменных 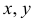 и
и 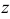 :
:
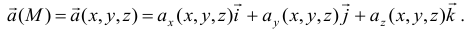
Векторной линией векторного поля называется кривая, направление которой в каждой точке 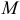 совпадает с направлением вектора, соответствующего этой точке поля.
совпадает с направлением вектора, соответствующего этой точке поля.
Потоком векторного поля, образованного вектором 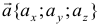 через поверхность
через поверхность 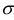 , называется поверхностный интеграл
, называется поверхностный интеграл
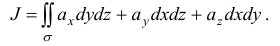
Если вектор 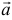 определяет поле скоростей текущей жидкости, то интеграл
определяет поле скоростей текущей жидкости, то интеграл 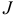 выражает количество жидкости, протекающей через поверхность
выражает количество жидкости, протекающей через поверхность 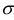 за единицу времени. При этом, если
за единицу времени. При этом, если 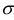 является замкнутой поверхностью, ограничивающей область
является замкнутой поверхностью, ограничивающей область 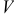 , и если интеграл
, и если интеграл 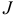 берется по внешней стороне
берется по внешней стороне 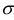 , то величина
, то величина 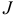 называется потоком вектора
называется потоком вектора 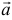 изнутри поверхности
изнутри поверхности 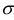 , она дает разность между количествами жидкости, вытекшей из области
, она дает разность между количествами жидкости, вытекшей из области 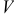 , и втекшей в эту область за единицу времени.
, и втекшей в эту область за единицу времени.
При 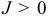 из области
из области 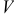 вытекает жидкости больше, чем в нее втекает, что указывает на наличие в этой области источников, питающих поток жидкости. При
вытекает жидкости больше, чем в нее втекает, что указывает на наличие в этой области источников, питающих поток жидкости. При 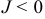 из области
из области 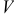 вытекает жидкости меньше, чем втекает, что указывает на наличие в этой области стоков, где жидкость удаляется из потока. При
вытекает жидкости меньше, чем втекает, что указывает на наличие в этой области стоков, где жидкость удаляется из потока. При 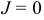 из области
из области 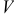 вытекает жидкости столько же, сколько в нее втекает.
вытекает жидкости столько же, сколько в нее втекает.
Дивергенцией векторного поля, определяемого вектором 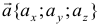 ,
,
называется скаляр
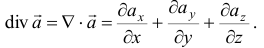
Если дивергенция в точке 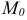 больше нуля (
больше нуля (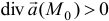 ), то эта точка называется источником, если
), то эта точка называется источником, если 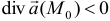 , то точка
, то точка 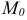 называется стоком. Абсолютная величина
называется стоком. Абсолютная величина 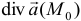 характеризует мощность источника или стока.
характеризует мощность источника или стока.
Векторное поле, во всех точках которого дивергенция равна нулю, называется соленоидальным. Поток такого поля через любую замкнутую поверхность равен нулю.
Формула Остроградского — Гаусса 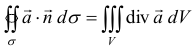 , где
, где 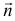 — внешняя нормаль к поверхности
— внешняя нормаль к поверхности 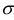 . В прямоугольных декартовых координатах формула Остроградского — Гаусса имеет вид:
. В прямоугольных декартовых координатах формула Остроградского — Гаусса имеет вид: 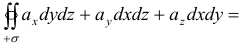
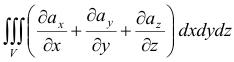 . Она устанавливает связь между потоком и дивергенцией векторного поля: поток векторного поля через замкнутую поверхность
. Она устанавливает связь между потоком и дивергенцией векторного поля: поток векторного поля через замкнутую поверхность 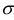 равен тройному интегралу по области
равен тройному интегралу по области 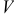 , ограниченной этой поверхностью, от дивергенции поля.
, ограниченной этой поверхностью, от дивергенции поля.
Ротором (или вихрем) векторного поля, определяемого вектором 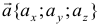 , называется вектор
, называется вектор
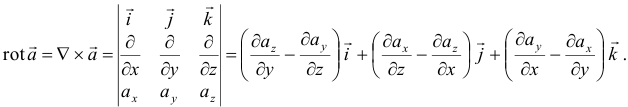
Запись ротора через определитель удобна для запоминания. Определитель обычно вычисляется разложением по первой строке (правая часть).
Векторное поле, во всех точках которого вихревой вектор равен нулю, называется потенциальным (или безвихревым). В потенциальном поле циркуляция всегда равна нулю.
Векторное поле, являющееся одновременно и соленоидальным и потенциальным, называется гармоническим.
Формула Стокса 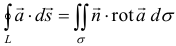 , где
, где 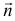 — нормаль к поверхности
— нормаль к поверхности 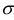 ,
, 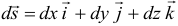 . Направление обхода контура
. Направление обхода контура 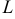 должно быть согласовано с выбранным направлением положительной нормали. Если наблюдатель смотрит с конца нормали, то он видит обход вдоль кривой
должно быть согласовано с выбранным направлением положительной нормали. Если наблюдатель смотрит с конца нормали, то он видит обход вдоль кривой 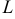 против часовой стрелки.
против часовой стрелки.
В прямоугольных декартовых координатах формула Стокса имеет вид
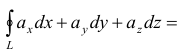
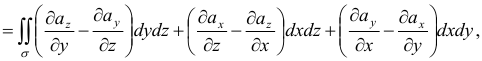
смысл которого заключается в следующем: циркуляция вектора по замкнутому контуру 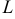 равна потоку вихря вектора через поверхность
равна потоку вихря вектора через поверхность 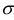 , ограниченную этим контуром.
, ограниченную этим контуром.
Пример:
Проверить, является ли векторное поле 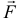 потенциальным или соленоидальным. В случае потенциальности поля
потенциальным или соленоидальным. В случае потенциальности поля 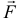 найти его потенциал, где
найти его потенциал, где 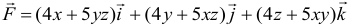 .
.
Решение:
Найдем дивергенцию векторного поля 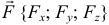 по формуле
по формуле 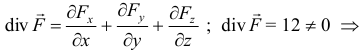 поле не является соленоидальным.
поле не является соленоидальным.
Найдем ротор векторного поля 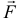 :
:
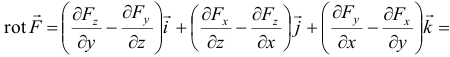
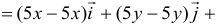
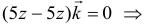 поле потенциальное.
поле потенциальное.
Найдем потенциал поля для функции, зависящей от трех переменных:
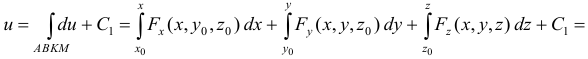
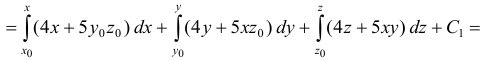
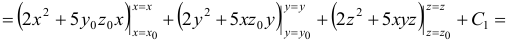
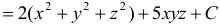 , где
, где 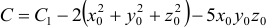 .
.
Ответ: векторное поле 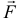 является потенциальным, его потенциал
является потенциальным, его потенциал 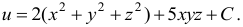
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Тройной интеграл |
| Криволинейный интеграл |
| Ряды в высшей математике |
| Определители матрицы: алгоритм, примеры вычисления |

