Оглавление:
Векторные линии поля
Рассмотрим векторное поле, задаваемое вектором 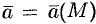 . Изучение поля удобно начинать с понятия векторных линий; они являются простейшими геометрическими характеристиками поля.
. Изучение поля удобно начинать с понятия векторных линий; они являются простейшими геометрическими характеристиками поля.
Векторной линией поля  называется линия, касательная к которой в каждой ее точке
называется линия, касательная к которой в каждой ее точке 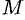 имеет направление соответствующего ей вектора
имеет направление соответствующего ей вектора 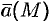 .
.
Это понятие для конкретных полей имеет ясный физический смысл. Например, в поле скоростей текущей жидкости векторными линиями будут линии, по которым движутся частицы жидкости (линии тока); для магнитного поля векторными (силовыми) линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Изучение векторного поля обычно начинают с изучения расположения его векторных линий. Векторные линии поля
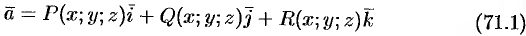
описываются системой дифференциальных уравнений вида
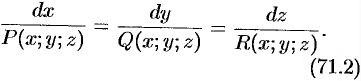
Действительно, пусть 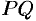 — векторная линия поля,
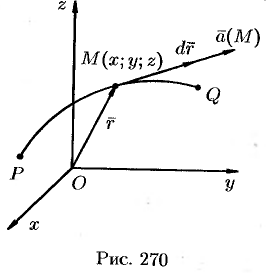
— векторная линия поля, 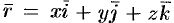 — ее радиус-вектор. Тогда вектор
— ее радиус-вектор. Тогда вектор 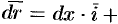
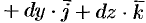 направлен по касательной к линии
направлен по касательной к линии 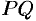 в точке
в точке 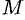 (см. рис. 270).
(см. рис. 270).
В силу коллинеарности векторов  и
и 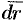 следует пропорциональность их проекций, т. е. равенства (71.2).
следует пропорциональность их проекций, т. е. равенства (71.2).
Пример №71.1.
Найти векторные линии поля линейных скоростей тела, вращающегося с постоянной угловой скоростью 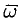 вокруг оси
вокруг оси 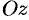 .
.
Решение:
Это поле определено вектором 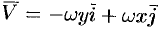 (см. пример 69.2). Согласно (71.2), имеем:
(см. пример 69.2). Согласно (71.2), имеем:
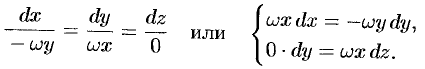
Интегрируя, получим: 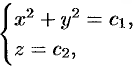 , т. е. векторные линии данного поля представляют собой окружности с центрами на оси
, т. е. векторные линии данного поля представляют собой окружности с центрами на оси 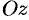 , лежащие в плоскостях, перпендикулярных к этой оси.
, лежащие в плоскостях, перпендикулярных к этой оси.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Поверхности и линии уровня скалярного поля |
| Производная по направлению скалярного поля |
| Поток векторного поля |
| Векторные дифференциальные операции первого порядка |

