Векторные дифференциальные операции первого порядка
Основными дифференциальными операциями (действиями) над скалярным полем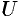 
и векторным полем 
являются 
, 
, 
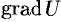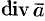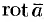. Действия взятия градиента, дивергенции и ротора называются векторными операциями первого порядка (в них участвуют только первые производные).
Эти операции удобно записывать с помощью так называемого оператора Гамильтона
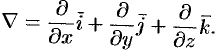
Этот символический вектор называют также оператором 
(читается «набла»); он приобретает определенный смысл лишь в комбинации со скалярными или векторными функциями. Символическое «умножение» вектора на скаляр 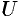или вектор производится по обычным правилам векторной алгебры, а «умножение» символов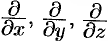 
на величины 
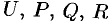понимают как взятие соответствующей частной производной от этих величин.
Применяя оператор Гамильтона, получим дифференциальные операции первого порядка:
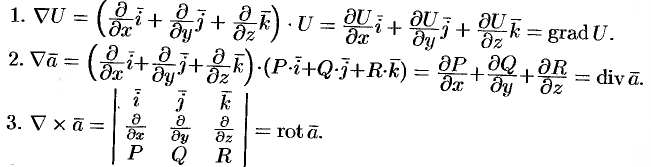
Оператор Гамильтона применяется для записи и других операций и для вывода различных формул в теории поля. При действиях с ним надо пользоваться правилами векторной алгебры и правилами дифференцирования.
В частности, производная по направлению (70.2) может быть записана в виде
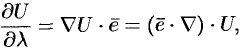
где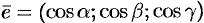 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Векторные линии поля |
| Поток векторного поля |
| Векторные дифференциальные операции второго порядка |
| Предел и непрерывность функции комплексного переменного |
