Оглавление:

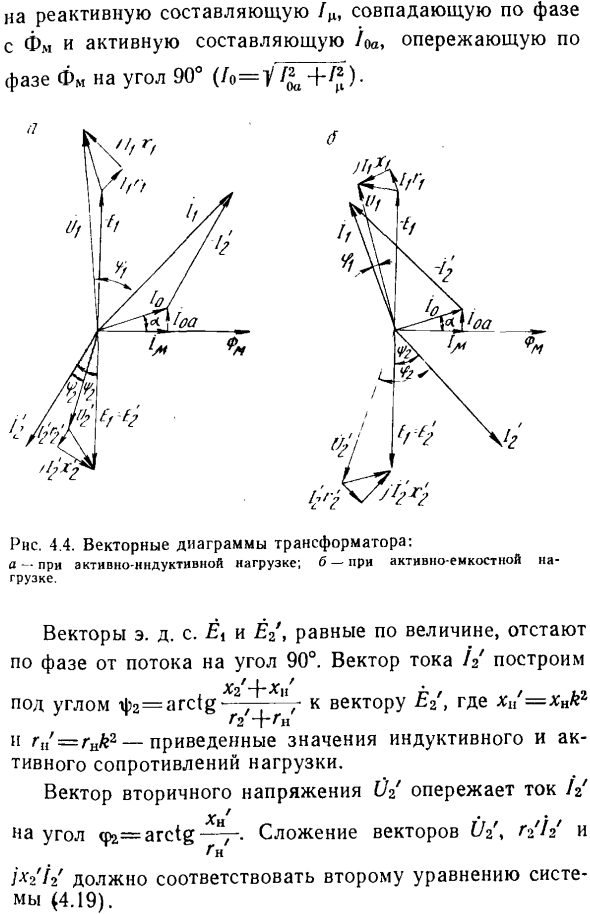


Векторные диаграммы трансформатора
Векторные диаграммы трансформатора. Комплексные уравнения трансформатора (4.19) и (4.20) могут быть представлены в виде векторной диаграммы. Создайте векторную диаграмму трансформатора с активной индуктивной нагрузкой 2″ = ri +} xn(рис. 4.4, а).
Это явное указание на связь между токами, напряжение обмоток и фазовый сдвиг между ними. Людмила Фирмаль
- Отложите основной вектор потока fm до положительного направления абсциссы. Нарисуйте вектор тока разомкнутой цепи / о под углом a к it. It разлагается на реактивные компоненты/ м. Фаза FM под углом 90°(/o = y / ^ + / 2). л-*для активной индуктивной нагрузки; Б-на активно емкостную нагрузку. Вектор e. d. s ^ 1 и E%, равные по величине, задерживают фазу от потока на угол 90°.
- Построить вектор тока Угол φ2=ось-к вектору 22 ?2 + ^ n И Hz ’ ^ hzk2-уменьшенное значение индуктивного сопротивления нагрузки и активного сопротивления нагрузки. Вторичный вектор напряжения Og больше, чем ток / V Xn Угол ψ −11ё -.Добавьте вектор 11g, Go ’/ g ’ и \ xnH должно соответствовать 2-му уравнению системы (4.19). ••» Исходя из Формулы (4.20), величина тока равна/ 1 = / 0 + (/g’).
В результате вектор тока I1 определяется геометрическим сложением тока I0 и составляющей I2′. Людмила Фирмаль
- Фаза обратного тока 1%、 Согласно первому уравнению системы (4.19)、 Вектор sum-Ei xL и] ’X \ 1′, получаем вектор приложенного напряжения 0 ^ ^ и угол сдвига φ! между Рами и 1 \ «векто». Аналогично вектор трансформаторов с активными емкостными нагрузками на Рис.1, рис. 4.4, б.
Смотрите также:
| Дифференциальные и комплексные уравнения однофазного двухобмоточного трансформатора. | Схема замещения. |
| Приведение величин в трансформаторе. | Режим холостого хода. |

