Оглавление:
Определение векторного произведения
Три некомпланарных вектора  ,
,  и
и  , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора
, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора  кратчайший поворот от первого вектора
кратчайший поворот от первого вектора  ко второму вектору
ко второму вектору  виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).
виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  , который:
, который:
1) перпендикулярен векторам  и
и  , т. е.
, т. е. 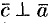 и
и 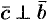 ;
;
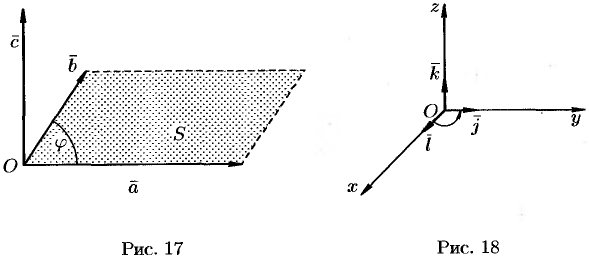
2) имеет длину, численно равную площади параллелограмма, построенного на векторах  и
и  как на сторонах (см. рис. 17), т. е.
как на сторонах (см. рис. 17), т. е.
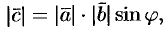 где
где 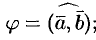
3) векторы  ,
,  и
и  образуют правую тройку.
образуют правую тройку.
Векторное произведение обозначается 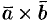 или
или 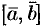 .
.
Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами 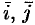 и
и 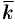 (см. рис. 18):
(см. рис. 18):
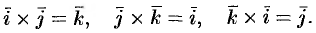
Докажем, например, что 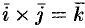 .
.
1) 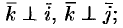
2) 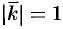 , но
, но 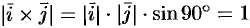 ;
;
3) векторы 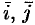 и
и 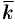 образуют правую тройку (см. рис. 16).
образуют правую тройку (см. рис. 16).
Свойства векторного произведения
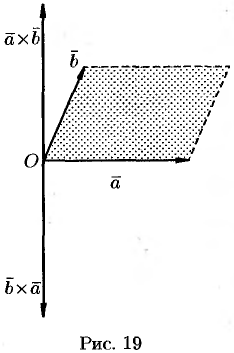
1. При перестановке сомножителей векторное произведение меняет знак, т. е. 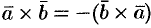 (см. рис. 19).
(см. рис. 19).
Векторы 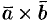 и
и 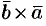 коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки
коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки 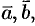
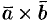 и
и 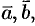
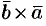 противоположной ориентации). Стало быть,
противоположной ориентации). Стало быть, 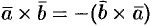 .
.
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. 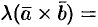
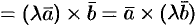 .
.
Пусть 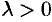 . Вектор
. Вектор 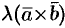 перпендикулярен векторам
перпендикулярен векторам 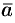 и
и 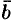 . Вектор
. Вектор 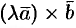 также перпендикулярен векторам
также перпендикулярен векторам 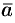 и
и  (векторы
(векторы 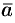 ,
, 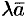 лежат в одной плоскости). Значит, векторы
лежат в одной плоскости). Значит, векторы 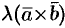 и
и 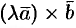 коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
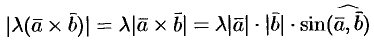
и
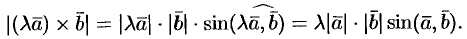
Поэтому 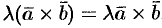 . Аналогично доказывается при
. Аналогично доказывается при 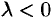 .
.
3. Два ненулевых вектора  и
и  коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е.
коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. 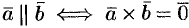 .
.
Если 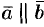 , то угол между ними равен
, то угол между ними равен 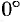 или
или 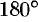 . Но тогда
. Но тогда 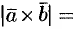
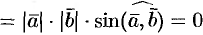 . Значит,
. Значит, 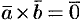 .
.
Если же 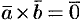 , то
, то 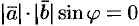 . Но тогда
. Но тогда 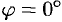 или
или 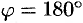 , т. е.
, т. е. 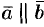 .
.
В частности, 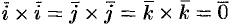 .
.
4.Векторное произведение обладает распределительным свойством:
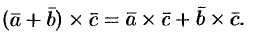
Примем без доказательства.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Выражение скалярного произведения через координаты |
| Некоторые приложения скалярного произведения |
| Смешанное произведение векторов |
| Основные приложения метода координат на плоскости |

