Векторная форма теоремы Остроградского-Гаусса

Векторная форма теоремы Остроградского-Гаусса

Векторная форма теоремы Остроградского-Гаусса. Сила действует на поверхность A (рис. 3.9), а плотность ее распределения (напряжение) показана в векторе pn. Сумма поверхностных сил, действующих на эту поверхность、 Мы поставили перед собой цель преобразовать этот Интеграл в Интеграл объема относительно V. To для этого разделите объем V на основные параллелепипеды с плоскостью, параллельной координате V.

Каждый из них взаимодействует с другим на контактной поверхности, но сила взаимодействия каждой поверхности определяется напряжением этой поверхности. Людмила Фирмаль

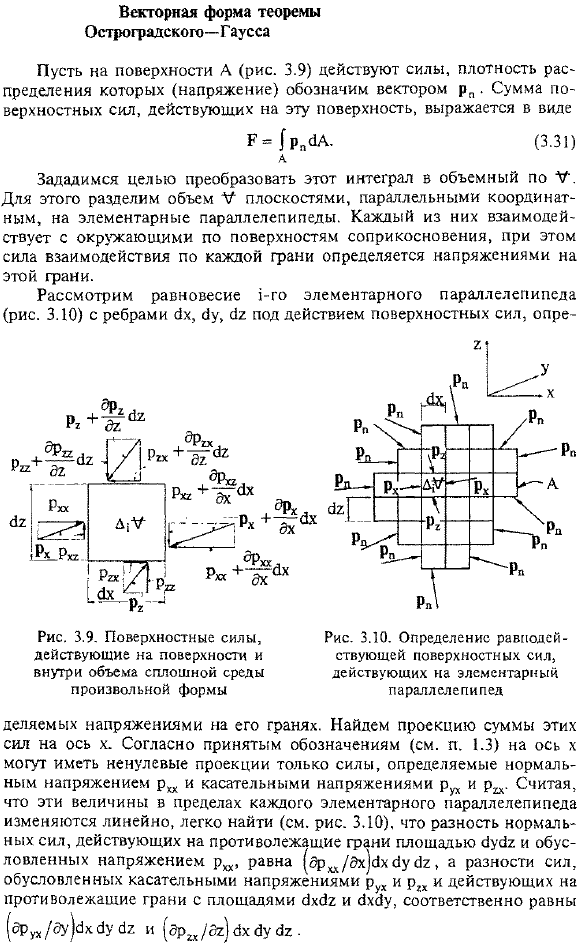
• Под действием поверхностных сил рассмотрим равновесие первого основного параллелепипеда (Рис. 3) с ребрами cx, ay, yr. Рис, 3.9.Поверхностные силы, действующие внутри поверхности и объема сплошной среды произвольной формы Лицо разделено стрессом. Найдите проекцию этих сил на ось X суммы. Согласно принятой системе счисления(см. раздел 1.3), ненулевую проекцию на ось x могут иметь только силы, определяемые нормальными и тангенциальными напряжениями px и p^.Предполагая, что эти значения изменяются линейно в пределах каждого базового параллелепипеда, область.

• Разность нормальных сил, действующих на противоположные поверхности, вызванная R и напряжением p ^(brxx / 3x / c! x yy yg, а также разность сил, обусловленных тангенциальными напряжениями pXX и p2X, и площадь Ohdg и c! Сила, действующая на противоположную сторону общая проекция силы на ось x равна То же самое рассуждение говорит вам о проекции результирующих поверхностных сил на оси y и Z. Из этих проекций можно сконфигурировать векторы DEG = DEPX * + D, Ru] + D, P2k. It представляется в виде столбцовой матрицы.

Вектор, который выражается в виде столбца тензорных расчетных зависимостей (3.32), называется расходимостью тензора напряжений P. (3.32) Где Д^ =ЗхЗуЗг объем первого параллелепипеда. Вектор D, P-результирующая сила всех поверхностных сил, действующих на базовую коробку. Рассмотрим сумму всех поверхностных сил DER, действующих на все основные параллелепипеды, в которых объем V равен divided.

В результате, когда все поверхностные силы суммируются, силы на контактной поверхности исчезают друг от друга, и ненулевой вклад в рассматриваемую сумму вносят только поверхностные силы, действующие на поверхность базового объема, которая не является контактной поверхностью смежного объема, принадлежащего объему V. Людмила Фирмаль

• Только поверхность базового объема совпадает с поверхностью A. Таким образом, сумма всех элементарных объемов, на которые делится V, D; D, будет равна равноденствию. Поверхностные силы функционирования геосистем Leica： Если мы одновременно рассмотрим сумму всех формул 1 в правой части уравнения(3.34), то легко увидим, что она равна Интегралу объема V вектора OM7.И так оно и есть.、 Согласно (1.18), поскольку pn = nP, (3.36) можно представить в виде: Это называется векторной формой теоремы острограда-Скай-Гаусса.