Вектор ускорения

Вектор ускорения

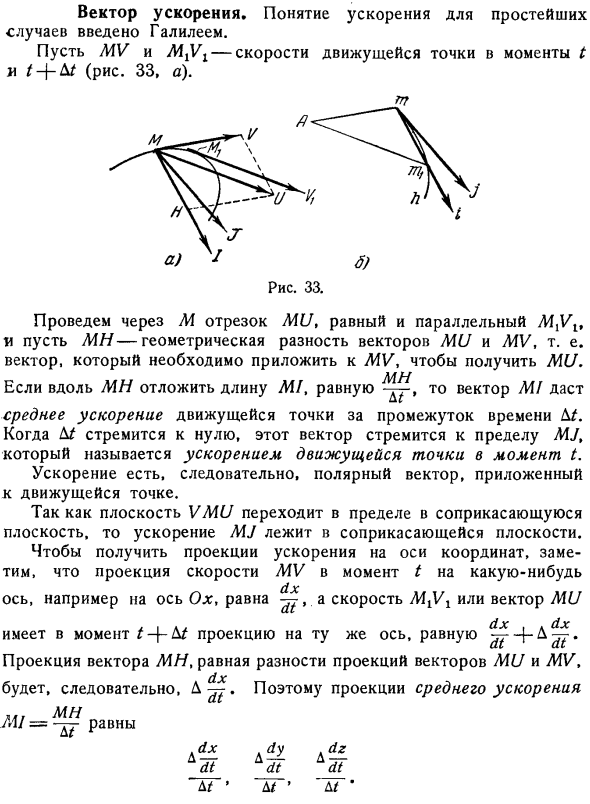
• Понятие ускорения в простейшем случае было введено Галилеем. Пусть MU и MgUx скорость движущейся точки в момент I и D рис. 33, а. Через M мы рисуем отрезок M, параллельный MN, равный Yi, и пусть MN вектор, который нам нужно применить к MU, чтобы получить геометрическую разницу между вектором MN и MU, то есть MN. Отложим в сторону длину M , равную a вдоль MH, и вектор M равен Среднее ускорение точки движения за определенный период D. Если Д стремится к нулю, то этот вектор стремится приблизиться к пределам MU, что называется ускорением точки движения в момент времени I. следовательно, ускорение является вектором полюса, приложенным к движущейся точке.

Плоскость Ми проходит границу контактной поверхности, поэтому ускорение ЛГУ находится на контактной поверхности. Проекция скорости движения MU в момент I для получения проекции ускорения на координатные оси Икс Например, ось оси Ox равна, А Вектор MI при скорости полета или моменте r + D проецируется на ту же ось, равную+.Таким образом, проекция вектора MN, равная разности между вектором MI и проекцией вектора MU, равна Д у… МГН M1 =равный Отсюда и проекция среднего ускорения. Предполагая, что D стремится к нулю, мы получаем значение в предсказании ускорения M time I. a2x ру Р аэаэ Ай Фотография: Joshua Roberts Getty ImagesThe понятие ускорения легко сводится к понятию скорости.

Рп величины этих векторов, причем эти величины будем считать положительными, если направления соответствующих векторов совпадают с направлением выбранной полупрямой, и отрицательными— в противном случае. Людмила Фирмаль

Нарисуйте вектор Am через любую фиксированную точку A. It параллельна, равна скорости MU точки движения во времени I рис. 33, б. Когда Я изменяюсь, вектор Am также изменяется, и его конечная точка образует новую движущуюся точку, которая представляет орбиталь A, называемую годографом. Скорость М этой новой движущейся точки в каждый момент времени равна ускорению точки M. In дело в том, что в момент 1 S точка m занимает позицию m1,а вектор Am одинаково параллелен вектору или M1.

• Вектор, параллельный VI или MH. Средняя скорость точки m во времени D это вектор m1 в направлении вдоль tm. Таким образом, эта средняя скорость m1 параллельна среднему ускорению M1 в точке M. когда предел достигнут, мы видим, что скорость m1 в точке m во времени I равна ускорению L4Y в точке M в то же время, когда D стремится к нулю. Например х = а 2 BA в до н. э, Г = Ц, 2 = Б + Б 1 с 1 Где a, b, c, a , b , c и, b , c константы. Траектория будет представлять собой параболу. Прогнозирование скорости = 2a + 4, = 2a + Ча Ж б, 2 Прогнозирование ускорения 3 Как видно, последнее является constant.

В результате ускорение остается постоянным по величине и направлению. А если, наоборот, величина и направление движения постоянны, то это движение определяется уравнением уравнения 1.фактически, на основе уравнения 3, путем последовательных интегралов, оно переходит сначала в уравнение 2, затем в уравнение 1.Такие движения более подробно изучаются при рассмотрении движения тяжелых предметов в вакууме.

Она эквивалентна также одному вектору, лежащему на центральной оси, и одной паре, плоскость которой перпендикулярна этой оси, т. Людмила Фирмаль

Важно отметить, что если величина и направление ускорения движения постоянны, то среднее ускорение любого периода а будет иметь одинаковую постоянную величину и direction. In фактически, когда уравнение 3 заполняется и вы интегрируете их, вы получаете уравнение 2.Из этого уравнения мы получаем те же значения 2a, 2a и 2a для проекции среднего ускорения времени A, что и для проекции ускорения времени I.

Смотрите также:

Предмет теоретическая механика

Произвольное прямолинейное движение; скорость	Касательное и нормальное ускорения (Гюйгенс)
Вектор скорости в криволинейном движении	Поступательное движение