Оглавление:






Ведение. классификация механических колебаний
- Начать с. Классификация механических колебаний Изучение колебательных процессов имеет важное значение для различных областей механики, физики и техники. Структура и вибрация машин, электромагнитные колебания в радиотехнике и оптике, звуковые и ультразвуковые колебания-все эти процессы сходны между собой по методу математической физики. Изучение этих колебаний очень важно для решения задачи прочности при переменных напряжениях. Давайте кратко обсудим основные понятия и зависимости, которые
должны работать в этой главе. Для того чтобы тело вибрировало, ему нужна определенная масса и упругость. Если упругое тело(нагруженная балка, скрученный вал или деформированная пружина) выведено из равновесного положения какой-то посторонней причиной (ударом, внезапной силой), то необходимо вывести его из равновесного положения. Все колебательные процессы, которые должны быть заполнены технологией, по этой классификации можно назвать кинематическими по внешним признакам, по форме законов, в которых определенное количество участвующих в процессе изменений изменяется со временем.
Это периодические и апериодические. В теории необходим Людмила Фирмаль
промежуточный класс (почти периодические колебания). Цикл-это процесс, в котором величина вибрации в любой момент времени после определенного времени T (периода) имеет одинаковое значение. Математическое определение периодической функции заключается в следующем. /(/+Л—П0 В любом значении переменной/. Апериодическая функция — это все остальные функции, которые не удовлетворяют заданным условиям. Почти периодическая
функция определяется следующим условиям Я/1(+)-А (01<е 526prime/где T и B являются конкретными константами. Вообще говоря, величина t, являющаяся функцией от e, называется почти периодом. Очевидно, что если Е очень мало по сравнению со средним значением модуля функции D ( / ) времени, то эта периодическая функция близка к периодической. Среди классов периодических колебаний основную роль играют синусоидальные колебания (синусоидальные
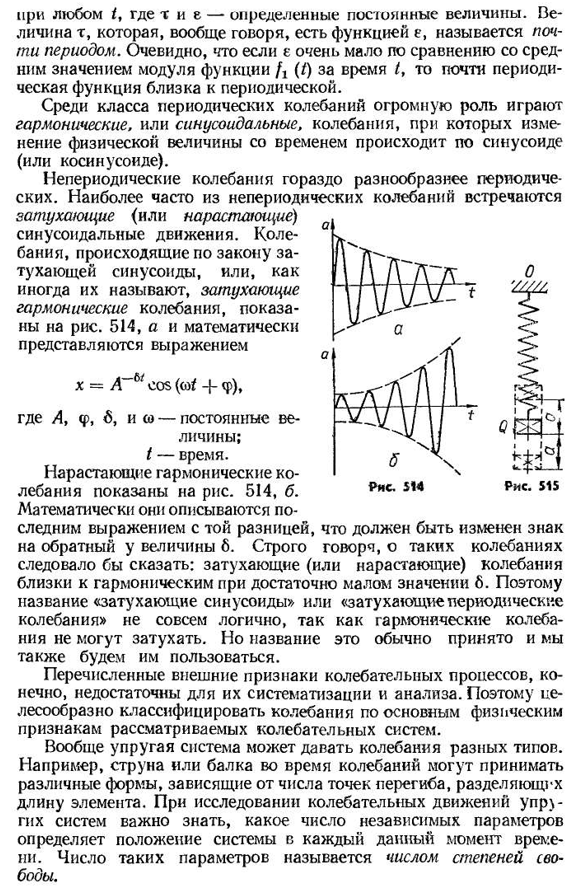
- колебания), когда изменение физических величин во времени носит синусоидальный (или кошиноидный) характер. Апериодические колебания гораздо разнообразнее периодических колебаний. Наиболее распространенным из апериодических колебаний является затухание (или увеличение) синусоидального движения. Колебания, возникающие по законам затухающей синусоиды, или, как их иногда называют, затухающие гармонические колебания, показаны на рисунке. 514, и и выражаются математически выражением т. x=a6z cos (<of -| — <p), A, f, fi и (o-постоянная; время. На рисунке показано увеличение гармонических колебаний. 514, род. Математически есть разница, что в последнем выражении необходимо изменить знак
на обратный значению 6. Строго говоря, о таких колебаниях надо сказать: затухающее (или увеличенное) колебание близко к гармоникам при достаточно малом значении B. Но название обычно принято и мы его тоже используем. Конечно, перечисленных внешних признаков колебательного процесса недостаточно для их систематизации и анализа. Поэтому рекомендуется классифицировать колебания в соответствии с основными физическими характеристиками рассматриваемой колебательной системы. В общем случае упругая система может давать различные типы колебаний. Например, струна или балка могут принимать различные формы во время вибрации, в зависимости
от количества точек перегиба, разделяющих длину элемента. При изучении Людмила Фирмаль
колебательного движения системы Ynpj важно знать ряд независимых параметров, определяющих положение системы в любой момент времени. Число таких параметров называется числом степеней свободы. 527 в простейшем случае положение системы можно определить только по одному значению. Ему дается степень свободы одной из систем, называемой системой. Рассмотрим простейший случай, показанный на рисунке. 515 если устройство допускает только вертикальное перемещение груза Q, а масса пружины меньше массы rpj на Q, то положение таких колебательных систем с определенной степенью свободы может определяться одним параметром, которым является вертикальное перемещение груза.
Система с более чем двумя степенями свободы, например, в системе, которая может характеризоваться двумя или более независимыми параметрами g и P2 в любой точке своего положения, существует пучок нулевой гравитации с двумя массами. 516,я). В качестве независимых параметров переменной- — Я. .. — _ масса t1 и T2 относительно положения pup и I — — — — «’» 7K Niu равновесие. учитывая поперечную вибрацию b-балки, можно постепенно присоединять ее к балке, увеличивая число степеней свободы- Рис отщение массы. На пределе получается балка с распределенной по всей длине массой(рис. 516,6} — система с бесконечными
степенями свободы. В этом случае отклонение в любой точке луча изменяется по специальным законам. С одной стороны, отклонение луча при колебаниях является функцией горизонтальной оси x, а с другой-непрерывной функцией времени. При классификации механических колебаний по другим характеристикам выделяют четыре возможных типа колебаний: естественные, вынужденные, параметрические и автоколебательные. Естественными (свободными) называются колебания, возникающие в изолированных системах вследствие внешнего возбуждения
(«удара»), вызывающего отклонения от исходного положения или начальной скорости системы. Типичным примером естественной вибрации упругой системы является вертикальная вибрация груза, подвешенного на конце пружины(рис. 515), если верхний край его зафиксирован и нагрузка отпущена после первого спуска. При собственных колебаниях характер колебательного процесса определяется только внутренними силами системы, в основном зависящими от ее физической структуры. Необходимая энергия, обеспечивающая процесс колебаний, поступает извне в ранние моменты возбуждения колебаний. Максимальное значение отклонения, то есть амплитуда колебаний и скорость собственных колебаний, определяется из начального значения 526 условия в этом
случае период колебаний (время полных колебаний) или частота колебаний, то есть обратная периоду, зависит от самой системы. Это значение уникально для системы и называется собственной частотой системы. Собственные колебания могут возникать не только вблизи устойчивого положения равновесия, но и в связи со стабильными движениями, например, крутильными колебаниями равномерно вращающихся валов. Во всех реальных системах машин требуется сопротивление колебательному движению (сопротивление среды, в которой происходит движение, трение подшипника, трение
соединений конструкции, сила внутреннего трения материала).) Это важная особенность собственных колебаний по сравнению с другими видами колебательного движения. Для упрощения теоретического исследования собственных колебаний в начале решения задачи силу сопротивления обычно игнорируют. Вынужденная вибрация называется упругой системой, и характер процесса системы извне, который наделен периодически изменяющимися мешающими силами, действующими непрерывно независимо от вибрации в системе, во многом зависит не только от характеристик системы,
но и от внешних сил. Примером вынужденной вибрации системы может служить поперечная вибрация балки (рис. 517), который служит опорой для электродвигателя, если его вращающаяся масса не полностью уравновешена. Период вынужденных колебаний равен периоду изменения мешающей силы. Амплитуда вынужденных колебаний не зависит от начальных условий. Хотя существует сила сопротивления, в отличие от его собственной вынужденной вибрации, не затухающей. Это связано с тем, что при силовых колебаниях в системе от возмущающей силы непрерывно поступает энергия, которая расходуется на преодоление существующего
сопротивления в системе. При известных условиях, если частота мешающей силы близка или совпадает с частотой собственных колебаний рассматриваемой системы, то вынужденная вибрация имеет значительную амплитуду (часто это явление называют резонансом). Параметрическими называются колебания упругой системы, при которых физические параметры системы периодически изменяются. Основные характеристики параметрических колебаний S29 заключается в том, что внешняя сила оказывает не прямое воздействие на колебательное движение, а на физические параметры системы.
Смотрите также:

