Задача 2.40.
В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено 19/3 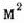 площади. На приобретение оборудования предприятие может израсходовать 10 тыс. руб., при этом оно может купить оборудование двух видов. Комплект оборудования I вида стоит 1000 руб., а II вида — 3000 руб. Приобретение одного комплекта оборудования I вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования II вида — на 4 ед. Зная, что для установки одного комплекта оборудования I вида требуется 2
площади. На приобретение оборудования предприятие может израсходовать 10 тыс. руб., при этом оно может купить оборудование двух видов. Комплект оборудования I вида стоит 1000 руб., а II вида — 3000 руб. Приобретение одного комплекта оборудования I вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования II вида — на 4 ед. Зная, что для установки одного комплекта оборудования I вида требуется 2 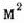 площади, а оборудования II вида— 1
площади, а оборудования II вида— 1 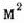 площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции.
площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции.
Решение:
Составим математическую модель задачи, Предположим, что предприятие приобретет 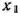 комплектов оборудования I вида и
комплектов оборудования I вида и 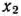 комплектов оборудования II вида. Тогда переменные
комплектов оборудования II вида. Тогда переменные 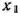 и
и 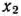 должны удовлетворять следующим неравенствам:
должны удовлетворять следующим неравенствам:
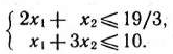
Если предприятие приобретет указанное количество оборудования, то общее увеличение выпуска продукции составит
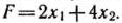
По своему экономическому содержанию переменные 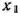 и
и 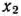 могут принимать лишь целые неотрицательные значения, т. е.
могут принимать лишь целые неотрицательные значения, т. е.
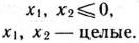
Таким образом, приходим к следующей математической задаче: найти максимальное значение линейной функции (25) при выполнении условий (24), (26) и (27). Так как неизвестные могут принимать только целые значения, то задача (24) — (27) является задачей целочисленного программирования. Поскольку число неизвестных задачи равно двум, решение данной задачи можно найти, используя ее геометрическую интерпретацию. Для этого прежде всего построим многоугольник решений задачи, состоящей в определении максимального значения линейной функции (25) при выполнении условий (24) и (26) (рис. 2.2)- Координаты всех точек построенного многоугольника решений ОАЕВС удовлетворяют системе линейных неравенств (24) и условию неотрицательности переменных (26). Вместе с тем условию (27), т. е. условию целочисленности переменных, удовлетворяют координа-
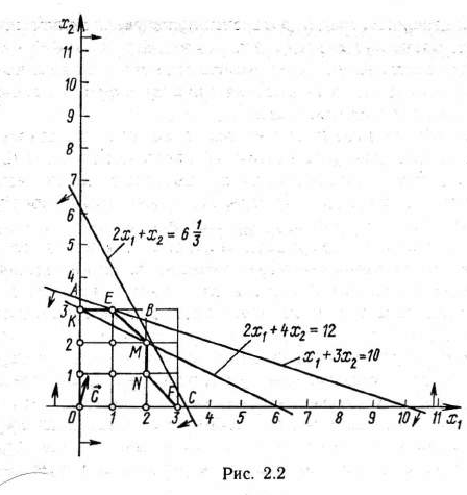
ты лишь 12 точек, отмеченных на рис. 2.2. Чтобы найти точку, координаты которой определяют решение исходной задачи, заменим многоугольник 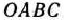 многоугольником
многоугольником 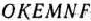 , содержащим все допустимые точки с целочисленными координатами и таким, что координаты каждой из вершин являются целыми числами. Значит, если найти точку максимума функции (25) на многоугольнике
, содержащим все допустимые точки с целочисленными координатами и таким, что координаты каждой из вершин являются целыми числами. Значит, если найти точку максимума функции (25) на многоугольнике 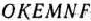 , то координаты этой точки и определят оптимальный план задачи.
, то координаты этой точки и определят оптимальный план задачи.
Для этого построим вектор 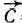 =(2; 4) и прямую
=(2; 4) и прямую 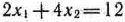 , проходящую через многоугольник решений
, проходящую через многоугольник решений 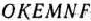 (число 12 взято произвольно). Построенную прямую передвигаем в направлении вектора
(число 12 взято произвольно). Построенную прямую передвигаем в направлении вектора 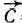 до тех пор, пока она не пройдет через последнюю общую точку ее с данным многоугольником. Координаты этой точки и определяют оптимальный план, а значение целевой функции в ней является максимальным.
до тех пор, пока она не пройдет через последнюю общую точку ее с данным многоугольником. Координаты этой точки и определяют оптимальный план, а значение целевой функции в ней является максимальным.
В данном случае искомой является точка 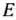 (1;3), в которой целевая функция принимает максимальное значение
(1;3), в которой целевая функция принимает максимальное значение 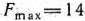 . Следовательно, координаты точки
. Следовательно, координаты точки 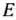 определяют оптимальный план задачи (24) — (27). В соответствии с этим планом предприятию следует приобрести один комплект оборудования I вида и три комплекта оборудования II вида. Это обеспечит предприятию при имеющихся у него ограничениях на производственные площади и денежные средства максимальное увеличение выпуска продукции, равное 14 ед. в смену.
определяют оптимальный план задачи (24) — (27). В соответствии с этим планом предприятию следует приобрести один комплект оборудования I вида и три комплекта оборудования II вида. Это обеспечит предприятию при имеющихся у него ограничениях на производственные площади и денежные средства максимальное увеличение выпуска продукции, равное 14 ед. в смену.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

