Оглавление:
Задача 4.1.
В распоряжение министерства, в подчинении которого находится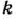 
предприятий, выделены средства в размере К тыс. руб. для использования их на развитие предприятий в течение 
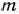лет. Эти средства в начале каждого хозяйственного года (т. е. в моменты 
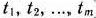) распределяются между предприятиями. Одновременно с этим между предприятиями распределяется полученная ими за прошедший год прибыль. Таким образом, в начале каждого 
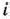-го года рассматриваемого периода 
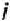-е предприятие получает в свое распоряжение 
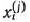тыс. руб. Задача состоит в определении таких значений 
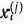,т. е. в нахождении таких распределений выделенных средств между предприятиями и получаемой ими прибыли, при которых за 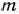лет обеспечивается получение максимальной прибыли всеми предприятиями.
Сформулировать поставленную задачу в терминах общей задачи динамического программирования.
Решение:
Предполагая, что 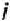-му предприятию на 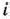-й год выделяется 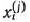тыс. руб., будем рассматривать данное распределение средств как реализацию некоторого управления 
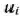. Таким образом, управление 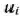состоит в том, что на 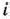-м шаге первому предприятию выделяется 
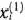тыс. руб., второму 
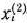,тыс. руб. и т. д. Совокупность чисел 
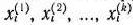определяет всю совокупность управлений 
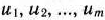на 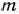шагах распределения средств как 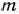точек в 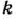-мерном пространстве.
В качестве критерия оценки качества выбранного распределения средств, т. е. реализуемых управлений, взята суммарная прибыль за 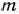лет, которая зависит от всей совокупности управлений:
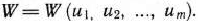
Следовательно, задача состоит в выборе таких управлений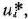 
т. е. в таком распределении средств, при котором функция 
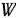принимает максимальное значение.
Как видно, сформулированная задача является многоэтапной. Эта многоэтапность определяется ее условиями, которыми предусмотрено принятие определенных решений в начале каждого года рассматриваемого периода времени. Вместе с тем в целом ряде других задач динамического программирования такая многоэтапность непосредственно не следует из их условий. Однако в целях нахождения решения такие задачи целесообразно рассматривать как многоэтапные. Приведем пример подобной задачи и дадим ее формулировку в терминах общей задачи динамического программирования.
Задача 4.2.
Для увеличения объемов выпуска пользующейся повышенным спросом продукции, изготовляемой предприятиями, выделены капиталовложения в объеме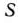 
тыс. руб. Использование 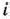-м предприятием 
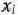тыс. руб. из указанных средств обеспечивает прирост выпуска продукции, определяемый значением нелинейной функции 
.
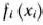Найти распределение капиталовложений между предприятими, обеспечивающее максимальное увеличение выпуска продукции.
Решение:
Математическая постановка задачи состоит в определении наибольшего значения функции
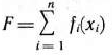
при условиях
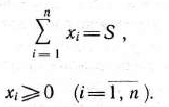
Сформулированная задача является задачей нелинейного программирования. В том случае, когда 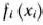— выпуклые (или вогнутые) функции, ее решение можно найти, например, методом множителей Лагранжа. Если же функции 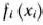не являются таковыми, то известные методы нахождения решения задач нелинейного программирования не позволяют определить глобальный максимум функции (1). Тогда решение задачи (1) — (3) можно найти с помощью динамического программирования. Для этого исходную задачу нужно рассмотреть как многоэтапную или многошаговую. Вместо того чтобы рассматривать допустимые варианты распределения капиталовложений между 
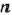предприятиями и оценивать их эффективность, будем исследовать эффективность вложения средств на одном предприятии, па двух предприятиях и т. д., наконец, на 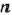предприятиях. Таким образом, получим 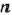этапов, на каждом из которых состояние системы (в качестве которой выступают предприятия) описывается объемом средств, подлежащих освоению к предприятиями 
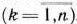. Решения об объемах капиталовложений, выделяемых 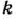-му предприятию 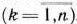, и являются управлениями. Задача состоит в выборе таких управлений, при которых функция (1) принимает наибольшее значение.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
