Задача №31.
В полый цилиндр радиуса 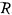 , способный катиться без скольжения по горизонтальной плоскости, вложен другой цилиндр радиуса
, способный катиться без скольжения по горизонтальной плоскости, вложен другой цилиндр радиуса 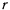 и веса
и веса 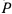 (рис. 4). На малый цилиндр, кроме силы тяжести, действует еще пара сил, расположенная в плоскости чертежа, с моментом
(рис. 4). На малый цилиндр, кроме силы тяжести, действует еще пара сил, расположенная в плоскости чертежа, с моментом  . На полый цилиндр намотана нить, которая на своем свободном конце несет груз веса
. На полый цилиндр намотана нить, которая на своем свободном конце несет груз веса 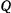 . Полагая поверхности цилиндров достаточно шероховатыми (чтобы не было скольжения), найти положение равновесия системы и определить, при какой зависимости между данными силами это равновесие возможно.
. Полагая поверхности цилиндров достаточно шероховатыми (чтобы не было скольжения), найти положение равновесия системы и определить, при какой зависимости между данными силами это равновесие возможно.
Решение:
Положение рассматриваемой системы можно определить двумя независимыми параметрами, в качестве которых выберем расстояние 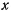 центра тяжести большого (полого) цилиндра от некоторой неподвижной вертикальной прямой и двугранный угол
центра тяжести большого (полого) цилиндра от некоторой неподвижной вертикальной прямой и двугранный угол 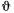 , образованный плоскостью, в которой расположены оси симметрии цилиндров, с вертикальной плоскостью. Нетрудно видеть, что выбранные параметры
, образованный плоскостью, в которой расположены оси симметрии цилиндров, с вертикальной плоскостью. Нетрудно видеть, что выбранные параметры 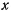 и
и 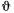 могут изменяться независимо один от другого и что при неизменных
могут изменяться независимо один от другого и что при неизменных 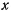 и
и 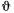 система не может совершать движений.
система не может совершать движений.
Сообщим системе такое возможное перемещение, при котором не изменяется угол 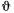 (при таком перемещении малый цилиндр будет вращаться вокруг своей оси симметрии, перемещающейся в горизонтальном направлении). Сила
(при таком перемещении малый цилиндр будет вращаться вокруг своей оси симметрии, перемещающейся в горизонтальном направлении). Сила 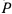 , действующая на малый цилиндр, при таком возможном перемещении не производит работы, и нам остается только подсчитать работу силы
, действующая на малый цилиндр, при таком возможном перемещении не производит работы, и нам остается только подсчитать работу силы 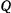 и пары
и пары  . Вертикальная сила
. Вертикальная сила 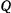 будет совершать работу, отличную от нуля, только тогда, когда груз перемещается в вертикальном направлении. При изменении координаты
будет совершать работу, отличную от нуля, только тогда, когда груз перемещается в вертикальном направлении. При изменении координаты 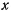 на величину
на величину 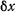 большой цилиндр повернется вокруг своей оси симметрии на некоторый угол
большой цилиндр повернется вокруг своей оси симметрии на некоторый угол 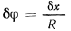 (этот угол на чертеже не указан). Спускающаяся часть нити при таком перемещении сократится на величину
(этот угол на чертеже не указан). Спускающаяся часть нити при таком перемещении сократится на величину 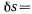
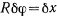 . Сила же
. Сила же 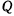 совершит работу —
совершит работу —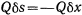 . Большой цилиндр повернется вокруг своей оси на угол
. Большой цилиндр повернется вокруг своей оси на угол  и относительное бесконечно малое перемещение точки
и относительное бесконечно малое перемещение точки 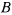 большого цилиндра (точки касания цилиндров) будет
большого цилиндра (точки касания цилиндров) будет 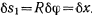 . Так как цилиндры не проскальзывают, то таким же по величине будет и относительное перемещение точки
. Так как цилиндры не проскальзывают, то таким же по величине будет и относительное перемещение точки 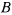 малого цилиндра. Поэтому малый цилиндр повернется вокруг своей оси на угол
малого цилиндра. Поэтому малый цилиндр повернется вокруг своей оси на угол
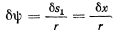
(угол на чертеже не указан). Пара сил, действующая на малый цилиндр, при таком повороте совершит работу
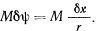
Работа же сил пары на поступательном перемещении малого цилиндра всегда равна нулю. Подсчитывая теперь работу всех сил, действующих на систему, и приравнивая эту работу нулю, будем иметь
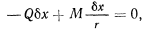
откуда получаем
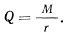
Сообщим системе такое возможное перемещение, при котором координата к не меняется, а меняется только угол 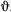 . При таком возможном перемещении сила
. При таком возможном перемещении сила 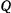 работы совершать не будет (отсутствует перемещение точки приложения силы). Работа же силы
работы совершать не будет (отсутствует перемещение точки приложения силы). Работа же силы  на рассматриваемом перемещении будет равна
на рассматриваемом перемещении будет равна
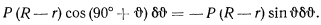
При вычислении работы пары сил заметим, что малый цилиндр на этом перемещении катится без скольжения по внутренней поверхности неподвижного большого цилиндра, вращаясь вокруг своей оси. Мгновенное перемещение малого цилиндра можно представить как сумму мгновенного поступательного перемещения вместе с осью 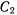 и мгновенного вращения вокруг этой оси. На поступательном перемещении пара сил работы не совершает. Если теперь обозначить угол поворота малого цилиндра относительно неподвижно ориентированных осей через
и мгновенного вращения вокруг этой оси. На поступательном перемещении пара сил работы не совершает. Если теперь обозначить угол поворота малого цилиндра относительно неподвижно ориентированных осей через 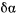 , то для изменения этого угла получим равенство
, то для изменения этого угла получим равенство
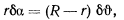
и работа сил пары будет равна
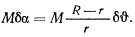
Подсчитывая работу всех активных сил и приравнивая ее нулю, из принципа возможных перемещений получим
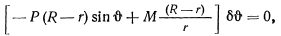
откуда следует условие для определения угла 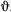 :
:
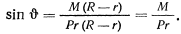
Действительное значение этого угла определяется только при выполнении условия
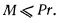
Принцип возможных перемещений позволяет дать обобщение принципа равновесия тяжелых тел, предложенного Торрнчелли, согласно которому центр тяжести системы тяжелых тел, находящихся в равновесии, занимает наинизшее из возможных положение. Из принципа возможных перемещений нетрудно получить, что при равновесии центр тяжести системы тел занимает стационарное положение. Этот принцип позволяет упростить исследование задачи о равновесии.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

