Оглавление:
Устранимые особые точки
Если 
— устранимая особая точка, то в окрестности точки разложение (76.11) имеет вид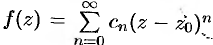 
. Это разложение справедливо во всех точках круга 
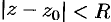, кроме точки 
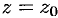. Если положить 
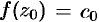, где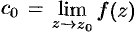 
(т. е. определить функцию 
в точке ), то функция станет аналитической во всем круге 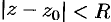(включая его центр 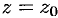); особенность точки устраняется, точка становится правильной точкой функции ).
Из равенства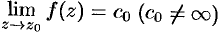 
следует, что в достаточно малой окрестности устраняемой особой точки функция является ограниченной.
Справедливо и обратное утверждение: изолированная особая течка 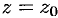является устранимой, если существует конечный предел 
.
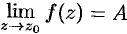Полюсы
Если — полюс, то в окрестности точки разложение (76.11) имеет вид
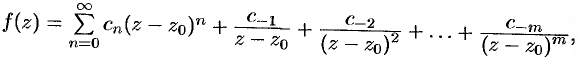
где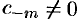 
. В этом случае полюс называется полюсом 
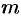-го порядка функции ; если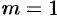 
, то полюс называется простым.
Запишем последнее равенство в виде
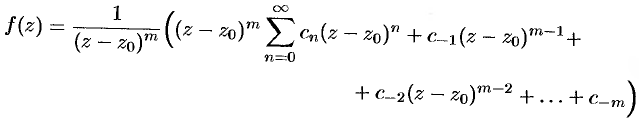
или
где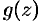 
— аналитическая функция, причем 
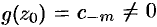. Отсюда следует, что 
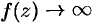при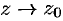 
, т. е. в достаточно малой окрестности полюса функция бесконечно велика.
Справедливо и обратное утверждение: изолированная особая точка 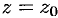является полюсом, если 
.
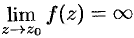Из равенства (76.16) имеем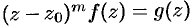 
. Отсюда получаем
удобный способ определения порядка полюса , если
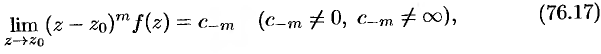
то точка есть полюс 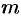-го порядка.
Имеется связь между нулем и полюсом функции.
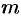Теорема 76.6. Если точка — нуль -го порядка функции , то является полюсом 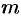-го порядка функции 
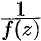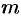; если точка — полюс -го порядка функции , то является нулем 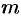-го порядка функции .
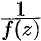Докажем первую часть теоремы. Пусть 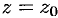есть нуль 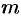-го порядка для функции . Тогда имеет место равенство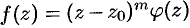 
, где 
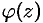аналитична в точке , причем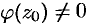 
. Тогда 
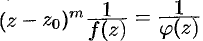и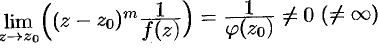 
. Это означает (см. (76.17)), что для функции 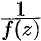точка 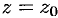является полюсом 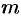-го порядка. Вторая часть теоремы (обратной) доказывается аналогично.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Нули аналитической функции |
| Классификация особых точек. Связь между нулем и полюсом функции |
| Существенно особая точка |
| Вычисление вычетов. Применение вычетов в вычислении интегралов |
