Оглавление:











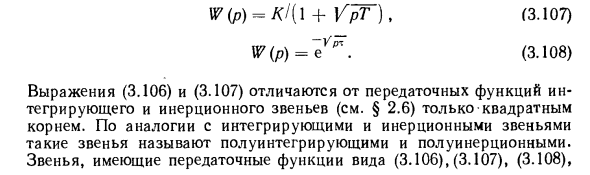


Устойчивость систем с запаздыванием и систем с иррациональными звеньями
- Устойчивость систем с задержками и нерациональными связями Система автоматического управления может включать в себя ссылки следующего вида, где взаимосвязь между величиной ввода u (t) и выходом y (t): 0 (0 = H (/ -T), (3,93) Где m — это постоянное значение, называемое временем задержки. Такие ссылки называются задержкой, потому что они дублируются б) t® о) • G Wap [P] W (P) W (P) Нзап (П) Рисунок 3.30. Количество входных данных изменяется без искажений, но существует постоянная задержка t. Функция передачи ссылки задержки (см. §2.6) ^ eap (P) = е — пирог (3,94) При использовании ленточного конвейера для перемещения материала из одной точки в другую, соединения с чистой задержкой распространены в различных технических процессах.
Система, которая регулирует толщину листа во время прокатки; Система автоматического управления, которая включает в себя, по меньшей мере, одну линию задержки, называется системой задержки. Процесс системы с задержкой описывается дифференциально-разностным уравнением. Используя сложное выражение функции передачи частоты без обратной связи W (/ (o)), определение критического времени задержки очень просто выполнить графически.
Условие Л (оКР) = — | UP (/ o) KP ) I = 1 — годограф W (j (.о) единица радиуса окружности с центром в начале координат (рис. 3.32). A), ^ и угол Людмила Фирмаль
1KP, (o2kR и (ozkg (Рис. 3.33))), система имеет некоторые важные времена задержки границы: t1kr = f (<‘> 1kr)’ Chkr; hgkr = Кkkr) / a> gkr; ^ zkr = ФКкр) / (ozkr, Минимальное время задержки составляет tkrt | n = t1KR. Система устойчива при m ^ cr и устойчива при T2kP <C cr. Система Как и tdnr, он становится нестабильным, когда tikp <C t <s t.jKP. Наблюдаемое в этом случае чередование участков устойчивости и нестабильности системы равно m (и другим Системные счетчики являются характерной особенностью многих систем с определенной задержкой. Обычно время задержки t требуется уменьшить, чтобы повысить скорость и точность системы.
Поэтому критерий устойчивости формулируется только для минимального времени задержки. Если время задержки t меньше минимального критического времени задержки t <tkrt | n, система автоматического управления стабильна. Важные времена задержки также могут быть легко определены при использовании логарифмов для проверки систем с задержками. Амплитудно-частотные (LLL) и фазово-частотные (LFH) характеристики. В этом случае круг с единичным радиусом представлен на горизонтальной оси. LAC системы с задержкой совпадает с LAC исходной системы без задержки. Дополнительный фазовый сдвиг, который необходимо учитывать при построении ФНЧ для системы с задержкой, определяется из (3.100).
- Пересечение LAH и горизонтальной оси определяет критическую частоту a) fKP, а запас по фазе (с учетом кратности), назначенный соответствующей критической частоте, определяет критическое время задержки TiKP. Связи с параметрами дисперсии, описываемыми уравнениями в частных производных, могут содержать передаточные функции вида: IV (p) = K / Vp ~, (3,106) (3,107) W (p) = eVpT. (3,108) Уравнения (3.106) и (3.107) отличаются от передаточных функций интегральной и инерциальной связей (см. §2.6) только квадратным корнем. По аналогии с интеграционными ссылками и инерционными ссылками такие ссылки называются полуинтеграционными и полуинерционными. Связи с передаточными функциями вида (3.106), (3.107), (3.108)
Это называется неразумной ссылкой. Выражение (3.108) не только иррационально, но и трансцендентно. Вам предстоит встретить необоснованные связи, учитывающие различные диффузионные и тепловые объекты, линии связи с потерями, распределенное сопротивление и пропускную способность. Стабильность замкнутых систем автоматического управления, включая принудительные связи, может быть исследована с использованием критериев устойчивости Найквиста.
Формулировка критерия устойчивости Найквиста в этом случае аналогична формулировке обычной системы автоматического управления, которая включает звенья, содержащие дробные рациональные передаточные функции. Людмила Фирмаль
Во многих тепловых процессах и процессах, когда сигналы передаются на расстояние с использованием длинных электрических, гидравлических и других линий, наблюдаются задержки, распределенные по длине линии, в отличие от чистых задержек Это приведет к искажению передаваемого сигнала. Для систем с распределенными единицами задержки, дифференциальные уравнения в частных производных необходимы для иллюстрации Во многих случаях решение уравнений в частных производных, показанных с учетом граничных условий, приводит к тому же типу системы, что и система с чистой задержкой, после некоторых упрощенных допущений всей системы автоматического управления. Получено дифференциально-разностное уравнение.
На практике аппроксимация передаточной функции сложных систем с распределением параметров широко используется с использованием передаточной функции систем с сосредоточенными параметрами и эквивалентной временной задержкой чистой задержки. Сложные системы высшего порядка с сосредоточенными параметрами, включающими множество инерционных связей, могут быть заменены для приближенных исследований более простыми системами более низкого порядка, но включают связи с чистой задержкой. В будущем будут рассматриваться только системы с чистой задержкой.
Блок-схема одноконтурной системы автоматического управления с одной линией задержки может быть представлена, как показано на рисунке 1. 3.30, и если линия задержки находится непосредственно в цепочке, или Рисунок 3.30, b, если линия задержки находится в цепи обратной связи. Передаточная функция открытой системы с задержкой (P) = wj (p) U7 (p) = Ш-е-г-9 (3,95) Q (P) Где W (p) = R (p) / Q (p) — передаточная функция без обратной связи и дробная рациональная функция оператора p. Если несколько линий задержки соединены последовательно в одноконтурной системе, они могут быть заменены одной линией задержки с эквивалентной постоянной времени задержки, равной сумме всех постоянных времен задержки.
Закрытая функция передачи системы, когда ссылка задержки находится непосредственно в цепи W = GPGG7 = — /? (P) e ~ P «y = (P) / D * CP> — (3.96a) Когда линия задержки находится в цепи обратной связи, передаточная функция замкнутой системы w ip) = = -t-_ JEldL. (3,966) ** ‘+’ >> Q (p, + R (p, e-> Dz (p) V ‘) Из (3.96a) и (3.966) видно, что характеристическое уравнение для системы с запаздыванием имеет вид: D-. (P) = Q (p) + R (p) = 0. (3,97) Это фактор е *? Характеристическое уравнение из-за существования Не является многочленом, но является трансцендентной функцией оператора p и имеет бесконечное число корней, в отличие от обычных алгебраических уравнений. с того времени e- «= I- £» + _ 4- е 1 В * -1- 2! 3! «» (3.97) можно рассматривать как уравнение «бесконечной степени».
Для того чтобы линейная система с постоянной задержкой была устойчивой, необходимо и достаточно, чтобы все корни уравнения (3.97) оставались. Поскольку найти корень уравнения (3.97) сложно, критерии устойчивости используются для проверки устойчивости систем с задержками. Обратите внимание, что обычные формы алгебраических критериев устойчивости Рауса и Гурвица не подходят для систем обучения с задержками. Кроме того, для устойчивости линейных систем,
Квадратичный и квадратичный с только положительным запаздыванием коэффициента характеристического уравнения Задержанные системы имеют множество критериев алгебраической устойчивости, которые похожи на критерии Рауса и Харвица, но не широко используются в инженерной практике из-за их относительной сложности. Для изучения устойчивости систем с задержками на основе принципа обсуждения или метода D-разбиения можно использовать эталон частоты для устойчивости Михайлова и Найквиста. Уравнение кривой Михайлова (годографа) системы с запаздыванием получается после подстановки p- / co в характеристическое уравнение (3.97). D, (/ co, e / wr) = Q (/ (o) -j-R (/ to) e «/ c) X = 0 (3,98)
Наличие коэффициента ε (3.98) делает контуры кривой Михайлова довольно сложными, и формулировка этого критерия для систем с задержками не так проста, как нормальная система. Ya. 3. Как показал Цыпкин, очень удобно изучать устойчивость систем с задержками, используя критерий устойчивости Найквиста. Заключение об устойчивости замкнутой системы с запаздыванием основано на изучении поведения амплитудно-фазовой характеристики Wx (yo>) открытой системы с запаздыванием по отношению к точке (-1, 0). В этом случае формулировка критерия устойчивости Найквиста для системы с запаздыванием аналогична формулировке нормальной системы с рациональной передаточной функцией дробей.
Передаточная функция частоты открытой системы Wt (/ co) с задержкой, p = / co (3,95) W, (f0) = W (f0) e «/ <, n = A (co) ef + (a>) e ‘, m = A (co) e ^ (tt>), (3.99) Здесь W (/ co) = U (co) -f / V (co) является амплитудно-фазовой характеристикой открытой системы, которая не учитывает задержку. L (co) = | UP (/ co) | = = U U2 (co) + V2 (co) — амплитудно-частотная характеристика. f (co) = -Arctg ——— Фазово-частотные характеристики открытой системы)) Без задержки ) проходит через точку (-1, 0). Время задержки TkP и соответствующее значение частоты ω ^ называются критическими, когда Wx (J (o) проходит через точку (-1, 0)).
Если серьезный, следующие условия выполняются: W, </ sr) = W (/ sr) e ~ / uVKP = A (sr) e ‘| Φ ~ «V ^ = -1 (3.10!) Условие (3.101) можно записать отдельно для амплитуды и фазы вектора W — (/ abr). W) Рисунок 3.31. A (сокращение) = | IM / Chr) | = 1 (3.102) <ККР) = + Кр) -coKPtKP = тс (2f + • 1), (3,103) Где я = 0, 1, 2, 3 ….. Из (3.102) вы можете сначала найти сокровище, затем из (3.103) вы можете найти xkP. FCSR) + «(» + 1) * + FCR) 2р. , 0 -scr = — = — H- и (3.104) Для систем автоматического управления с задержками минимальное критическое время задержки является наиболее важным
(I = 0), это на той же временной границе VKp) 7t -J-Arc tg- xKD = — = — = -, {6.1U0) КР кр шкр ‘> кр’ Где φ () = 4- /’ a> D). Следовательно, условие в этом случае (3.102) Iy7. (/ K KP) Hf * / (i + KrLV = / (/ KG + ^ rT ™ = 1). Найти критическую частоту из последнего уравнения 0, cr = / JfTTl / r, / s> I. Критическая частота фазового сдвига L («cr) = -arc tg o> crG = -arc tg Найти критическое время задержки из UK1-1. (3.105). it-Arc tg // (2-1 ^ k-Arc tg UK * -1 —2- = Т ОЦК // (2-я
Смотрите также:
Примеры решения задач по теории автоматического управления

