Оглавление:



Устойчивость центрально-сжатых стержней. Общие положения.
- Центральная стабильность Компрессионный Стержень Как отмечается в главе 14 общих положений, помимо расчета прочности и жесткости строительных конструкций и их элементов для восприятия сжимающих напряжений, необходимо также рассчитывать устойчивость. Из теоретической механики известно
, что положение равновесия абсолютного твердого тела является устойчивым, индифферентным и неустойчивым(рис. 24.1, а, в, с). В сопротивлении материала, помимо положения равновесия, учитывается равновесие системы в деформированном состоянии. Например, гибкий линейный
стержень под действием небольшой Людмила Фирмаль
сжимающей осевой силы находится в устойчивом равновесии. Когда этот стержень изгибается под действием нескольких поперечных нагрузок, а затем удаляется, стержень возвращается в исходное состояние линейного равновесия (рис. 24.2, а). Если осевая сжимающая сила превышает определенное значение, линейное
равновесие становится неустойчивым и заменяется криволинейным. 24.2, б). Стабильность, таким образом, позволяет конструкции сохранять свое исходное положение или деформированное состояние равновесия и совершать его с небольшими отклонениями после устранения причин, вызвавших эти отклонения. Существует
- устойчивое равновесное положение и устойчивость стержня равновесной формы в деформированном состоянии. Первый относится к достаточно жестким конструкциям,например, подпорным стенам, башням. Второе относится к гибкой конструкции, выполненной из эластичного материала. Выход структуры из начального состояния равновесия называется потерей устойчивости.
Небольшая избыточная нагрузка, способная к наличию новой устойчивой равновесной формы, называется критической нагрузкой и обозначается ГКР. Критическая сила — это наименьшее значение центральной силы сжатия, при которой стержень теряет способность сохранять свое первоначальное равновесное состояние.
Потеря устойчивости вследствие качественного изменения деформации- Людмила Фирмаль
267al «Л»» 7 7W7M 777/77 Рис. 24.1 рис. 24.2 Первая форма равновесия называется первым видом потери устойчивости или потерей устойчивости Эйлера. В новой форме равновесия за счет качественного изменения деформированного состояния в конструкции (элементах) возникают дополнительные напряжения, которые не обеспечиваются обычным расчетом прочности. Эти дополнительные напряжения могут вызвать структурные потери при внешних нагрузках от силы равновесия. Явление потери
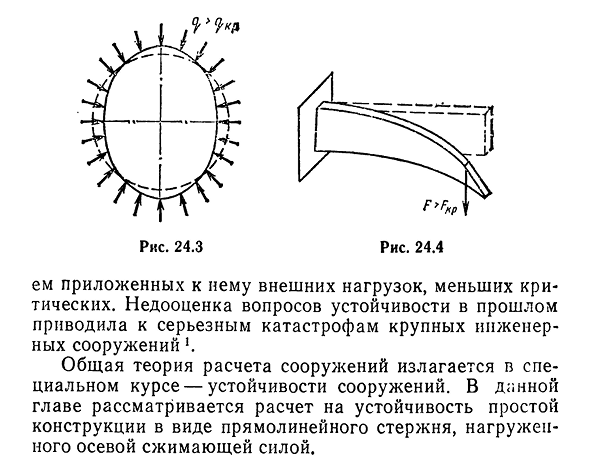
устойчивости возникает внезапно, поэтому его трудно предотвратить с помощью неправильно назначенных конструкций размеров уплотняемых элементов. Линейный стержень, в котором осевая сжимающая сила меньше критической, действует только на сжатие, а при силе, большей критической, он с меньшей вероятностью вызывает сжатие и изгиб из-за кривизны оси. Потеря устойчивости первого рода происходит и во многих других случаях. Например, при критическом значении гидростатического давления круговая форма кольца становится неустойчивой и принимает форму эллипса в
новом равновесном состоянии (рис. 24.3). Консоль с тонкостенным прямоугольным сечением, изогнутая в вертикальной плоскости, теряет свою первоначальную форму при критическом значении изгибающего момента, а на балке в горизонтальной плоскости появляются дополнительные изгибы и кручения (24.4). Изучение устойчивости конструкций и определение критических нагрузок имеет большое практическое значение для создания надежных конструкций. Для обеспечения сохранности конструкции она должна
обеспечивать стабильность исходного равновесного состояния при действии.- 68,000, £ 24.3 м Никакая внешняя нагрузка не добавила к нему, меньше критического. Недооценка проблем устойчивости прошлого привела к массовым инженерным катастрофам!. Общая теория расчета конструкции изложена в специальном курсе-устойчивость конструкции. В этой главе описывается расчет устойчивости простой конструкции в виде линейного стержня, нагруженного осевыми сжимающими силами.
Смотрите также:
Решение задач по технической механике
| Нормальные напряжения при внецентренном сжатии (растяжении) | Формула Эйлера |
| Ядро сечения | Влияние способа закрепления концов стержня на критическую силу |

