Оглавление:





Устойчивость сжатых стержней основные понятия
- Устойчивость сжатого стержня Основное понятие В предыдущих главах рассмотрены методы определения напряжений и деформаций растяжения, сжатия, кручения и изгиба. Установлены также критерии прочности материалов со сложным сопротивлением.
Однако во многих случаях при проектировании инженерных сооружений обычной прочности конструкции недостаточно, чтобы получить полную картину работы сооружения.
Зная, что напряжение не превышает расчетного сопротивления материала, все же не дает Людмила Фирмаль
права делать вывод о безопасности существования конструкции. Помимо вопроса о прочности, существует вопрос о так называемой устойчивости конструкции или ее элементов. Инженерный объект, помимо нагрузки, учитываемой расчетами, всегда испытывает небольшое воздействие (возмущение), которое заставляет тело
двигаться из расчетного равновесного или кинетического состояния. Если малые возмущения вызывают небольшие отклонения системы от расчетного(не возмущенного) состояния, то это состояние системы является устойчивым. Наоборот, при малых возмущениях, когда
- происходит большое отклонение системы от расчетного состояния, последняя неустойчива. Хорошим примером стабильного или неустойчивого состояния является вращение нормальной спиновой вершины (гироскопа). Хорошо известно, что чем быстрее скорость вращения волчка, тем больше сопротивление попыткам отвлечь его от ВР- 457 страницы 384D Вращение вокруг вертикальной оси. Таким образом, вращательное движение верха при больших скорос
относительно малых возмущений является устойчивым. Когда скорость вращения падает ниже определенного значения, те же самые небольшие возмущения резко меняют его состояние, вызывая неустойчивые движения. Поэтому на малой скорости движение верха становится неустойчивым. Примером устойчивого или неустойчивого равновесия может служить тяжелый шар,
лежащий на вогнутой или выпуклой сфере(рис. 384). В первом случае (рис. 384, а) Людмила Фирмаль
при небольших отклонениях шар стремится вернуться в исходное состояние. Источник и отклоненное состояние шара мало чем отличаются друг от друга. В последнем случае(рис. 384, б) при любом незначительном отклонении шарик скатится вниз. Возмущения и заданное состояние шара резко отличаются друг от друга. Шар в нижней части вогнутой сферы находится в устойчивом равновесии, а в верхней части выпуклой сферы его равновесие становится неустойчивым. Аналогичное явление наблюдается при изучении
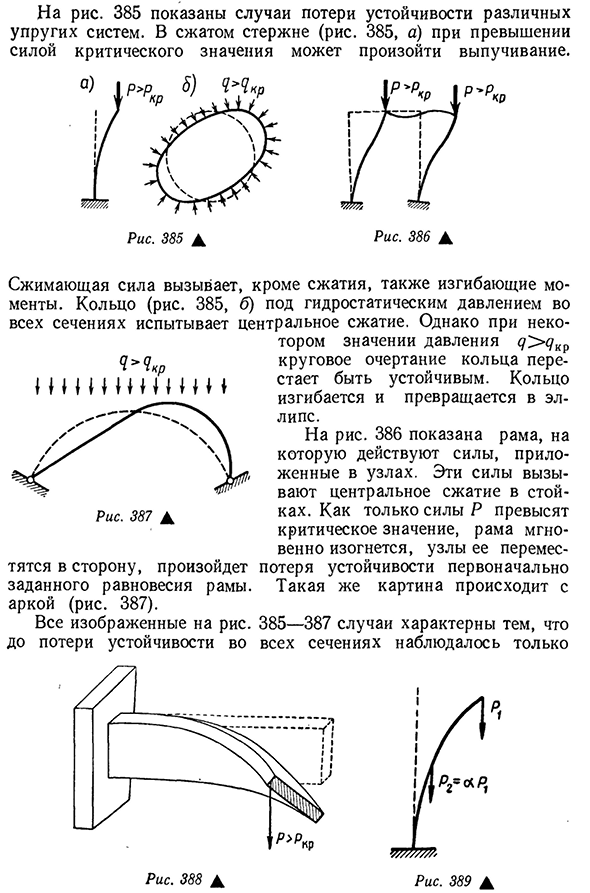
равновесия сжатого стержня. При меньшем усилии сжатия, чем критическое значение PDCR круговая форма кольца становится неустойчивой. Кольцо согнется и превратится в овал. Для риса. 386 указывает кадр, в котором действует сила, приложенная к узлу. Эти силы вызывают центральное сжатие на стойке. Как только сила Р превышает критическое значение, рама мгновенно прогибается, и происходит ее сдвиг-потеря устойчивости в виде рамы, дуги(рис. 387). Все показано на рисунке. 385-387 случаев характеризуются тем, что до
потери устойчивости на всех участках наблюдались только Рис 388А Я Рис 389А 460центральное сжатие. В момент потери устойчивости изгиб прикрепляется к центральному сжатию. Система переходит из одного равновесного состояния в другое. Происходит потеря устойчивости при Центральном сжатии. Для риса. 388 показан еще один случай потери устойчивости. Сначала балка изгибается в вертикальной плоскости (плоский изгиб). Как только сила превышает критическое значение, плоская форма изгиба становится неустойчивой, в горизонтальной плоскости возникают дополнительные изгибы и кручения. Аналогично, потеря
устойчивости может происходить при кручении, сжатии центра и других видах деформации. Если система нагружена не одной, а несколькими силами или какими-то сложными нагрузками, то выбирается один параметр, и вся система сил нагружается двумя силами, например, этой (рис.). 389), сила P2 выражается в терминах (P2=с помощью множителя a. следовательно, она берется как параметр,которому дана вся мощность. Определив критический параметр P1kr и зная a, мы можем узнать всю критическую нагрузку такого стержня.
Смотрите также:

