Оглавление:






Устойчивость равновесия системы
- После того как точки системы информируются об очень малых начальных отклонениях от положения равновесия и очень малых начальных скоростях, притирки системы материальных точек называются устойчивыми, если система последующих движений отклоняется очень мало от рассматриваемого положения равновесия. Посвящена исследованию голономной, установившейся и равновесной устойчивости систем, подчиненных идеальной связи. Если такая система находится в поле консервативных сил, то устойчивость равновесия системы определяется в соответствии с теоремой Лагранжа Дирихле или теоремой Ляпунова.
Вот теорема Лагранжа-Дирихле если потенциальная энергия минимальна в положении равновесия системы, то положение равновесия устойчиво. Потенциальная энергия системы может быть разбита на ряд степеней обобщенных координат. Это разложение начинается со второго или большего члена, связанного с координатой, если положение равновесия принимается за начало координат, а потенциальная энергия положения равновесия принимается равной нулю. L определить устойчивость равновесия, если величина потенциальной энергии в положении равновесия не минимальна. М.
Прямой называется задача, и которой по заданным движению и массе материальной точки определяется равнодействующая сил, приложенных к этой точке. Людмила Фирмаль
Применить теорему Ляпунова. А если минимальный недостаток потенциальной энергии можно определить в члене 2-го порядка i расширения потенциальной энергии, то равновесие системы неустойчиво без учета членов более высокого порядка. Б если потенциальная энергия максимизируется в положении равновесия, то равновесие системы становится неустойчивым. Это может быть установлено путем рассмотрения членов высшего порядка 1, которые фактически существуют в серии разложений потенциальной энергии. При решении задачи об устойчивости равновесия системы с 1 степенью свободы под действием потенциальных сил рекомендуется следующая процедура.
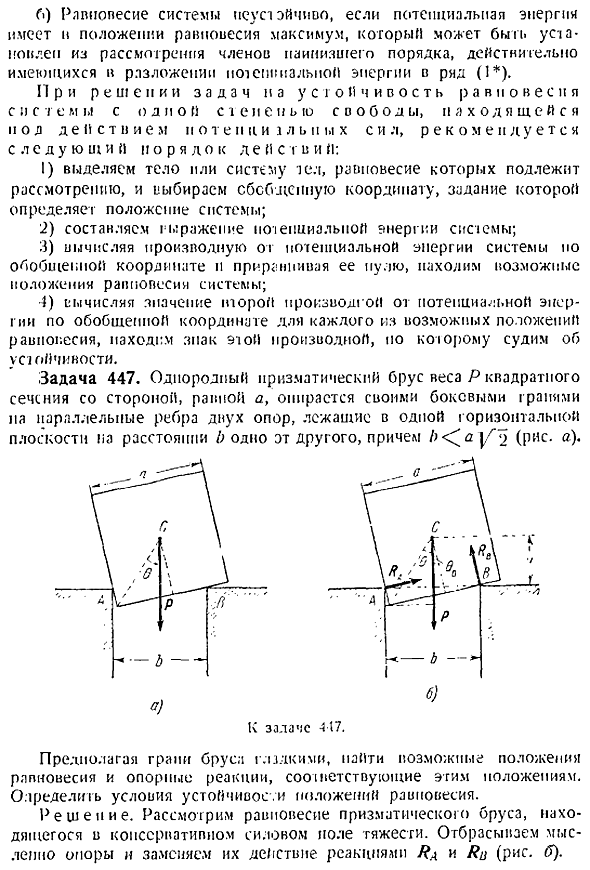
Выберите систему объектов или объектов, в которых рассматривается равновесие, и выберите обобщенные координаты. Его задача определяет местоположение системы. 2 выразить потенциальную энергию системы 3 найти возможное положение равновесия системы путем вычисления производной позиционной энергии системы по обобщенным координатам и уравнивания ее с пулей. 4 найти знак этой производной путем вычисления значения 2-й производной энергии положения по обобщенным координатам для каждого из возможных положений равновесия, определив тем самым устойчивость. Задача 447.
Однородная призменная балка с массой квадратного сечения p, стороны которой равны q, представляет собой b a pys-a, опирающуюся на стороны и параллельные ребра двух опор, лежащих на расстоянии друг от друга на одной и той же горизонтальной поверхности. Предполагая, что края пучка гладкие, находим возможные положения равновесия и вспомогательные реакции, соответствующие этим положениям. Определите условие устойчивости положения равновесия. Решение.
- Рассмотрим равновесие призменного пучка, который находится в поле действия консервативных сил гравитации. Мысленно отбросьте опору и замените действие реакцией ra и pc рисунок b, затем выберите обобщенные координаты, определяющие положение луча. Для обобщенных координат возьмем угол 6, который образуется диагональю вертикального сечения вертикальной балки. Найдите высоту и центр тяжести над прямой ab рисунок b. Или И Л И О, потому что- 2 2 Б s1p в Соз 0о 0о h — pop 0 — 51 p 2 oo. 2 2 1 2 Углы 9 и 0 20, −20 И так оно и есть. И-cos 0-zs 2-o u2 2 и Или Потому что в.
Потому что потенциальная энергия гравитации равна произведению веса на высоту P P-и Затем, когда дается 5, это выглядит так А Р — cos0—потому что 20 У2 2 Найдите производную по P 6 и уравняйте ее с нулем .—— Я — 2б cos0 81P0 0 .6 R bGO 2 1 y 1 Из этого уравнения мы видим, что возможны 2 положения равновесия .Первое положение равновесия будет 31n0 0 или 0 0 .2-е равновесие —4-cos0 0, или G и Соз 0 — — — — Т — 2 U 2 это положение равновесия возможно, если 7 Найти вторую производную потому что 9 — — 2В, потому что 29 .У Один П СОС а 0а Для решения задачи устойчивости равновесия необходимо найти знак этой производной для каждого из возможных равновесий positions .In первая позиция 9 9 0.
С помощью дифференциальных уравнений движения материальной точки можно решать две основные задачи динамики: прямую и обратную. Людмила Фирмаль
Подставляя это значение в формулу 10, получаем м 2Д — Ч Поэтому, по теореме Лагранжа-Дирихле, это положение является Если Новосибирск стабилен 12 В противном случае положение равновесия является unstable .At 2-е положение равновесия, in e, agsso — .Подставляя это значение угла в выражение 10, находим 1 .северный .П 6а о е, б 13 14 13 Один Но согласно 9 G-2 0- Поэтому мы приходим к выводу, что 403 .16 То есть положение равновесия 6 9 неустойчиво согласно теореме 2-го Ляпунова .Исключение составляет 9 0 и −2 0 Четыре 17 Это соответствует первому положению равновесия, рассмотренному ранее .Возможные положения равновесия твердых тел могут быть определены другим способом .Определите угол 9, чтобы создать 3 уравнения равновесия для любого положения луча рисунок B .
Первое уравнение-это равенство суммы проекций всех сил на горизонтальную ось нулю .dso5b0 — B5teo 0 .18 2-е уравнение равно нулю суммарной проекции всех сил на вертикальную ось .Я 31П 0о- -Кос — П-0 19 3-е уравнение-это уравнение к нулю суммы моментов силы относительно точки D .20 Из формул 18 и 19 видно, что Р cos0 .21 Подставляя это значение в Формулу 20, получаем ПБ КОС 2 22 Или Б потому что 20 градусов-81P 0 0 2 2 23 0 0 U2 24 25 И напоследок 1 пенс за доллар 26 Значение, соответствующее 2 возможным положениям равновесия 0, равно 1 nO 0 n, следовательно 0 01 0 2 conv — C, следовательно 0 02 a.
Первое решение соответствует симметричному положению балки, где плоскость балки наклонена под углом 45 градусов относительно горизонтальной плоскости .2-е решение возможно в случае 2b 2 .если a 2 2, то находим cos0 1, то есть 81n6z 0, и возвращаемся к первому случаю .Найти величину реакции в первом возможном положении равновесия 27 28 2-е положение равновесия а-я — 8 — р ХАА — Б а г П .
Смотрите также:
Предмет теоретическая механика

